Una Estrategia Alternativa para la Solución del Problema

Retomando el problema y el contexto presentado, digamos que en nuestra paciente, después de tener en cuenta en ella cerca de nueve variables o datos (edad, género, raza, sitio, nivel de atención, edad de menarquia, edad del primer nacido vivo, antecedentes familiares de cáncer de seno y realización de biopsias de mama), hemos llegado a la estimación de una probabilidad basal (pretest) de cáncer de mama del 0.12%.

La paciente trae una mamografía, que ostenta una sensibilidad de 87% y una especificidad de 89%, la cual es reportada como positiva.

La pregunta en busca de espera sigue siendo la misma: “Dada la existencia de una probabilidad pre-prueba del 0.12% y una mamografía positiva (con 87% de sensibilidad, 13% de falsos negativos, 89% de especificidad y 11% de falsos positivos), qué tan probable es (probabilidad pos-prueba) que nuestra paciente realmente tenga cáncer de seno?”

De manera concisa, el método Bayesiano toma esos tres porcentajes y los inserta en una formulación matemática para establecer la respuesta. Existe creciente evidencia, que enseñar a estudiantes de medicina y a clínicos en ejercicio, el razonamiento Bayesiano en términos de probabilidades, no alcanza adecuado y sostenido aprendizaje con aplicaciones poco útiles en la práctica clínica17 .

Un método alternativo muy ingenioso, desarrollado por Gigerenzer y Hoffrage18 , sobrelleva estas dificultades. Ellos lograron demostrar, que el desempeño en la inferencia Bayesiana podría ser mejorada considerablemente al cambiar una parte importante del trabajo: LA REPRESENTACIÓN DE LA INFORMACIÓN19. Ellos proponen representar la información estadística en un formato que denominaron frecuencias naturales.

Nuestro problema expresado en frecuencias naturales sería así:

De 10.000 mujeres de 45 años, 12 podrían desarrollar cáncer de seno. De esas 12 mujeres, 10 podrían recibir un resultado positivo de una mamografía para cáncer de mama. De las 9988 mujeres de 45 años que no desarrollan cáncer de mama, 1099 mujeres reciben un resultado de mamografía positivo para cáncer. Imagínese una nueva muestra de pacientes de 45 años que reciben un resultado de mamografía positivo: ¿Cuántas realmente tienen cáncer de seno?

¿Cómo encontramos esas frecuencias naturales y cómo le damos respuesta a la pregunta?.

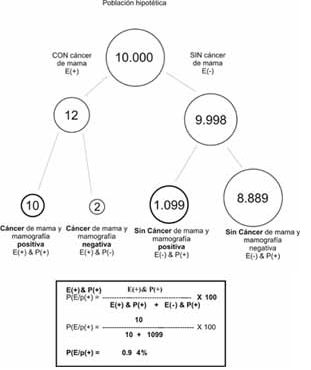
Los pasos son los siguientes, que se grafican en la figura 3:

Figura 3. Representación de la información para la inferencia Bayesiana, mediante el formato de frecuencias naturales.

1. Seleccione una población hipotética suficientemente grande (p.ej. 10.000) y multiplique esa cifra por la probabilidad basal (pre-prueba) de cáncer de seno de la paciente. En nuestro caso 0.12% de 10.000 es 12 mujeres.

2. Tome ese resultado (12 mujeres) y use la sensibilidad de la prueba, para determinar cuántas mujeres tienen la enfermedad y la prueba positiva (87% de 12 es aproximadamente 10 mujeres).

3. Tome el número restante de personas que no están enfermas (9.988) y use la proporción de falsos positivos para determinar cuántos no están enfermos pero tienen la prueba positiva (11% de 9988 es aproximadamente 1099).

4. Compare el número obtenido del paso 2 con la suma de los pasos 2 y 3, para determinar cuántas mujeres con mamografías positivas realmente están enfermas mediante la siguiente ecuación:

P(E/p(+)) =((E(+) & P(+))/(E(+) & P(+)) + (E(-) & P(+)) )* 100

Donde P(E/p(+))es la probabilidad de cáncer dado un resultado de la mamografía positivo (probabilidad pos-prueba), E(+) & P(+), son las mujeres con cáncer y mamografía positiva (producto de la sensibilidad por la probabilidad pre-prueba), y E(-) & P(+) son las mujeres sin cáncer pero con mamografía positiva (producto de la probabilidad pre-prueba de no estar enfermo por la proporción de falsos positivos).

Como se aprecia en nuestro ejemplo, 10 mujeres de cada 1.109 tienen cáncer de seno (menos de 1% de probabilidad pos-prueba), cifra bastante distante de la que cualquiera hubiese podido calcular con métodos exclusivamente creativos. Para concluir, diremos entonces, que en mujeres de 45 años con los antecedentes enunciados, y con una probabilidad pre-prueba del 0.12%, la presencia de una mamografía positiva incrementó su probabilidad, ahora probabilidad pos-prueba, a casi un 1% (exactamente 0.9%).

Convenciones: E(+): Enfermedad presente, E(-): Enfermedad ausente, P(+): Prueba positiva, P(-): Prueba Negativa. P(E/p(+)):Probabilidad de enfermedad dada una prueba positiva (probabilidad pos-prueba). E(+) & P(+): Enfermedad y prueba positiva, E(+) & P(-): Enfermedad y prueba negativa, E(-) & P(+): No enfermedad y prueba positiva, E(-) & P(-): No enfermedad y prueba negativa

Ya que la probabilidad se incrementó, pero quedó ubicada aun en un valor de la escala de probabilidades extremadamente bajo, es muy claro que la mamografía, aun con un resultado positivo no ha ayudado de manera significativa para la toma de una decisión (resecar la lesión vs. tranquilizar y olvidarse del tema) en esta paciente, y este valor se convertirá ahora en la probabilidad pre-prueba de próximos datos.

Si quisiésemos en éste momento apelar a otra prueba diagnóstica, deberíamos utilizar alguna con una sensibilidad muy cercana al 100% (inexistente en el cáncer de seno) con el objeto de que, si sale negativa, descarte, por el momento, esta enfermedad. Desafortunadamente la mayoría de las pruebas diagnósticas en cáncer de mama son más específicas que sensibles1 .

Por otro lado, asumamos por un instante, sólo con fines pedagógicos, que nuestra paciente tiene otros factores de riesgo, que la ubican en una probabilidad pre-prueba inicial del 10%. A cuánto ascendería su probabilidad pos-prueba si tuviese una mamografía positiva?. Intente dar una respuesta siguiendo los pasos anteriores utilizando el mismo rendimiento de la mamografía.

En éste caso la probabilidad ascendió a 47% (espero que haya coincidido) y quedó colocada ahora en un punto adecuado para ser confirmado por una de las tantas pruebas específicas existentes.

Queda entonces claro, que el principal elemento en la función Bayesiana es el valor de la probabilidad pre-prueba, que es cambiante de país a país y de nivel de atención..

Digamos para concluir, que ante condiciones poco prevalentes (con probabilidades pre-prueba muy bajas), que suelen presentarse en niveles primarios de atención ambulatorio o comunitario, se deben seleccionar dentro del arsenal disponible las pruebas diagnósticas con alta sensibilidad esperando un resultado negativo para descartar. En este caso, resultados intermedios ascienden muy poco dicha probabilidad pre-prueba.

Por otro lado, en condiciones muy prevalentes, como las que suelen verse en hospitales de III y IV nivel, deberían utilizarse pruebas altamente específicas con el fin de confirmarlas dado su resultado positivo. La negatividad de pruebas en ese escenario, reduce muy levemente dichas probabilidades pos-prueba.

El problema diagnóstico realmente es de los clínicos, y es formidable cuando quiera que las incertidumbres reinantes acerca de una enfermedad se encuentren aun a mitad de camino de sus umbrales de confirmación o de exclusión. Desafortunadamente éste último escenario es la forma más frecuente de presentación de los pacientes con sus enfermedades o molestias en la práctica clínica cotidiana.

El presente capítulo, pertenece al libro: “La ciencia y el arte del proceso diagnóstico: Una aproximación desde la Medicina Basada en Evidencias”®, de Jairo Echeverry Raad, que será publicado en el 2004. Está siendo cedido sin cargo, para ser utilizado por los lectores de la Revista Colombiana de Neumología. Para uso personal y académico exclusivamente. Cualquiera otra utilización requiere permiso explícito del autor. Todos los derechos reservados.

Bibliografia

1. Mushlin AF. Diagnostic test in breast cancer: Clinical strategies based on diagnostic probabilities. Ann Intern Med 1985:1030-79.
2. Brown ML, Houn F, Sickles EA, Kessler LG. Screening mammography in community practice: positive predictive value of abnormal findings and yield of follow-up diagnostic procedures. AJR Am J Roentgenol 1995; 165:1373-7.
3. Echeverry J, Ardila E. Pruebas Diagnósticas y Proceso Diagnóstico. En: Estrategias de Investigación en medicina Clínica. Ardila E, Sánchez R, Echeverry J. Editores. 1ª Edición 2000. El Manual Moderno. Bogotá; Capítulo 13.
4. Echeverry J. Definiendo Enfermedad. Rev Col Neumol 2003; 15(2):69-81.
5. Sox HC, Blatt MA, Higgins MC, Marton JI. Medical Decision Making. Butterworths Publishers, 1988. Boston USA; Chapter two.
6. Nkanginieme KEO. Clinical Diagnosis as a Dynamic Cognitive Process: Application of Bloom’s Taxonomy for Educational Objectives in the Cognitive Domain. Med Educ Online [serial online] 1997; 2:1. Available from: URL https://www.utmb.edu/meo/
7. Godolphi W. The role of risk communication in shared decision making. BMJ 2003;327:692-3.
8. TM. Abdelhamid. The Multidimensional Learning Model: A Novel Cognitive Psychology-Based Model for Computer Assisted Instruction in Order to Improve Learning in Medical Students. Med Educ Online [serial online] 1999;1,1. Available. URL https://www.Med-Ed-Online.org.
9. Kahneman D, Slovic P, Tversky A. eds. Judgment under uncertainty: heuristic and biases. Cambridge: Cambridge Univ Press, 1982.
10. Tvuersky A, Kahneman D. Judgment under uncertainty: heuristic and biases. Science 1974;185:1124 – 31.
11. Slotnik HB, Mejicano G, Passin SM, Bailey A. The epidemiology of physician learning. Medical Teacher 2002; 24(3):304-12.
12. Miller GA. The magic number seven plus or minus two: some limits on our capacity for processing information. Psychol Rev 1956;63:81-97
13. Sox HC, Blatt MA, Higgins MC, Marton KI. Medical Decision Making. Boston: Butterworth Publishers, Boston USA. Chapter three. 1988.
14. Sox HC, Blatt MA, Higgins MC, Marton JI. Medical Decision Making. Butterworths Publishers, Boston USA. Chapter four. 1988.
15. Hoffrage U, Linsey S, Hertwig R, Gingerenzer G. Commutating statistical information. Science 2000;290:2261-62.
16. Steuer J, Fischer JE, Bachmann LM, Soller M, Riet Gt. Communicating accuracy of test to general practitioners: a controlled study. BMJ 2002;324:824-26.
17. Hirsch R, Riegelman RK. Probability. In: Hirsch R, Riegelman R Eds. Statistical First Aid: Interpretation of Health Research Data. Blackwell Scientific Publications, USA. 1992. Pp 3 –20.
18. B. Fundamentals of Biostatistics. Duxbury Press. California USA. 3ª edition. 1990:51 – 59.
19. Gingerenzer G, Edwards A. Simple tools for understanding risks: from innumeracy to insight. BMJ 2003;327:741-44.
20. https://cebm.jr2.ox.ac.uk/
21. Feuer EJ, Wun LM, DevCan:probability of developing or dying of cancer. 4.1. Bethesda, Md.: National Cancer Institute, 1999.
22. Sox HC. Exercise testing in suspected coronary artery disease. Disease-a- month. December 1985.
23. McGee S. Evidence-based physical diagnosis. W.B. Saunders Company. Philadelphia, PA, USA. 2001
24. Wasson JH, Sox HC, Goldman L, Neff RK. Clinical Prediction Rules: applications and methodologic standards. N Engl J Med 1985; 313:193 – 200.
25. https://bcra.nci.nih.gov/brc/
26. The Women’s Health Initiative. Risks and Benefits of Estrogens Plus Progestin in Healthy Postmenopausal Women: Principal Results From the Women’s Health Initiative Randomized Controlled Trial. JAMA 2002; Vol.288 (3):321-333.
27. Fletcher S, Elmore JG. Mammography screening for breast cancer. N Engl J Med 2003;348:1672-80.
28. Sacket DEL, Haynes RB, Tugwell P. Clinical Epidemiology. A basic science for clinical medicine. Boston: Little, Brrown and Company 1985.
29. Knapp RG, Miller MC. Describing the Performance of a Diagnostic Test In:. Knapp RG, Miller MC. Clinical epidemiology and biostatistics. Malvern (Pennsylvania): Harwal Publishing Company, 1992: 31 –51.
30. Suchman AL, Dolan JG. Odds and Likelihood Ratio. In: Griner, Panzer RJ, Greenland P, eds. Clinical diagnosis and the laboratory . Logical strategies for common medical problems. Chicago: Year Book Medical Publisher, 1986:36 –43.
31. Yerushalmy J. Statistical problems in assessing methods of medical diagnosis with special reference to X-ray techniques. Public Health Reports 1947;62:1432 – 1449.
32. Olsen O, Gotzsche PC. Cochrane review on screening for breast cancer with mammography. Lancet 2001;355:129-34.
33. Brown ML,Houn F,Sickles EA,Kessler LG. Screening mammography in community practice: positive predictive value of abnormal findings and yield of follow-up diagnostic procedures. AJR Am J Roentgenol 1995;165: 1373-7.
34. Elmore JG, Barton MB, Moceri VM, Polk S, Arena PJ, Fletcher SW. Ten-Year Risk Of False Positive Screening Mammograms And Clinical Breast Examinations. N Engl J Med 2003; 338(16): 1089 -96
35. Seldmeier P. Improving statistical reasoning: theoretical models and practical implications. Mahwah NJ,Lawrence Erlbaum. 1999.
36. Gigerenzer G, Hoffrage U. Using natural frequencies to improve diagnostic inferences. Academic Medicine 1998;73:538-40.
37. Fletcher S, Elmore J. Mammography screening for breast cancer. N Engl J Med 2003;348(17):1672-80.