El Universo y La Muestra

El Universo y la Muestra

Los estudios observacionales trabajan con muestras para determinar la asociación entre la variable de exposición (factor de riesgo) o de desenlace (enfermedad).

El universo es toda la población a la cual se va a estudiar, de la cual, por razones prácticas y con fundamento estadístico se extrae una muestra.

Por muestra, se entiende a una selección de la población, que puede ser, dependiendo de sus características, no probabilística (por conveniencia), o probabilística (aleatoria, estratificada, o por conglomerados).

Las muestras no probabilísticas son muy y mal usadas en los diseños epidemiológicos observacionales.

Un ejemplo claro son las muestras extraídas de encuestas a transeúntes en una calle, que si bien pueden ser ‘aleatorias’, no son representativas de una población.

Muchos estudios epidemiológicos declaran muestras probabilísticas cuando en realidad usan muestras por conveniencia.

Existen varios tipos de muestreo probabilístico.

En el muestreo aleatorio simple, todos los sujetos deben tener la misma probabilidad de ser elegidos. Es muy común en escenarios cerrados, como hospitales, cárceles y escuelas.

Es uno de los muestreos más usados en epidemiología por su fácil obtención, a pesar de esto, es susceptible de sesgos de selección si no se eligen bien los sujetos.

Por ejemplo, si una patología (como en infarto agudo al miocardio) es más frecuente y/o severo a una hora determinada del día, no se pueden elegir solo pacientes de unas horas determinadas (por ejemplo, durante el ‘día’).

El muestreo estratificado es un método complejo de selección de pacientes, en el cual se dividen los sujetos por una determinada característica, a la que se le asigna una probabilidad; dentro de la cual se toma una muestra aleatoria simple.

El muestreo por conglomerados se puede dividir en dos: monoetápico, y estratificado polietápico. El primero se realiza idealmente en poblaciones dispersas, por conjuntos geográficos.

El polietápico se realiza cuando la población a cubrir es muy grande y ampliamente distribuida.

Ambos requieren de técnicas estadísticas especiales, disponibles en algunos paquetes estadísticos informáticos (por ejemplo: Epi- Info, SPSS, Stata, SAS).

Diseños Observacionales

Los estudios observacionales pueden llegar a ser muy eficientes para descubrir o lanzar hipótesis determinantes o factores de riesgo para una enfermedad, sin llegar a dilucidar en la inmensa mayoría de los casos, la causa de las mismas.

Al mismo tiempo, sus alcances y metodologías pueden ser limitantes de tal forma que los invalidan a la luz de los conocimientos epidemiológicos y estadísticos actuales.

Dependiendo del tipo de diseño observacional a utilizar, los estudios observacionales tienen ventajas y desventajas que los hacen útiles para exposiciones poco frecuentes (estudios de cohorte), enfermedades raras (estudios de casos y controles), o para ganar eficiencia en la generación de hipótesis (estudios transversales).

Los estudios que mayor nivel de evidencia proveen son los estudios de cohortes, le siguen los de casos y controles, y finalmente, abajo en los niveles de evidencia epidemiológica se encuentran los transversales.

Estudios trasversales o cross-sectional: estos determinan la prevalencia de una enfermedad dada en un momento singular del tiempo, con casos nuevos y viejos.

En este tipo de estudio, la variable de exposición no está sujeta al control del investigador, por lo que es difícil determinar su grado de envolvimiento en el desenlace.

Son muy útiles para generar nuevas hipótesis acerca de un componente causal, sin llegar a confirmarlo.

Dadas sus características, este tipo de estudio es muy eficiente, y es uno de los más comunes en epidemiología.

Pero esa eficiencia lleva un costo: la temporalidad, necesaria para confirmar la causalidad.

No se puede determinar y no se sabe que fue primero, si la variable de exposición o de desenlace.

Es por esto que en estos estudios, se omite la definición de causalidad, y se prefiere la de asociación, para dejar claro que lo que se encontró fue una relación estadística entre una variable de exposición y otra de desenlace.

El análisis de este tipo de estudios se puede realizar mediante test estadísticos que miran la asociación más allá del azar o estimadores epidemiológicos.

Teniendo en cuenta que para evaluar asociaciones que evalúen factores confusores se necesitan modelos multivariados que miren varias variables independientes.

Muchos test estadísticos existen para comparar la asociación entre las variables de exposición y desenlace. Cada uno se utiliza dependiendo del tipo de variable y su tipo de distribución de probabilidad.

El principal indicador de la asociación más allá del azar es el valor de P, que por consenso, se establece que un valor menor de 0,1, 0,05, ó 0,01, indica una relación más allá del azar. Es decir una asociación propiamente dicha.

Uno de los estimadores epidemiológicos más utilizados en estudios es Odds Ratio (OR) o razón de momios.

Es un número que indica el riesgo proporcional de presentar un desenlace, con relación a una exposición.

Los valores de 0 a 1 indican un factor protector con relación al desenlace (a un valor de 0,4, se reduce la probabilidad del desenlace un 60%), y los valores mayores de 1 indican un factor de riesgo con relación al desenlace (a un valor de 1, 4, se aumenta la probabilidad del desenlace un 40%).

En teoría, el OR puede alcanzar el infinito, pero raras veces alcanza un valor de 100, a menos que existan sesgos o variables de confusión que lo afecten.

Existe una discusión epidemiológica acerca de la capacidad analítica de los estudios transversales.

Sin embargo, a la luz del conocimiento actual, si la temporalidad de una exposición está bien documentada en un estudio transversal, no existen impedimentos que limiten su capacidad de realizar análisis que puedan generar hipótesis para luego ser comprobadas por estudios más complejos.

Es así, que se han diseñado y validado diferentes modelos matemáticos para este tipo de estudios.

Estudios de casos y controles: el uso y entendimiento de los estudios de casos y controles ha sido uno de los más importantes avances de la epidemiología moderna (2). Su diseño es complejo y su entendimiento no es fácil.

En vez de partir desde la exposición, se comienza desde el desenlace, llamándose ‘caso’ el paciente con desenlace, y ‘control’ el paciente sin el desenlace.

A cada grupo se le busca evidencia previa de la exposición. Esto ha hecho que se le llamen retrospectivos, cuando en realidad pueden ser prospectivos o ambispectivos (retrospectivo y prospectivo al mismo tiempo), dependiendo de cómo se realicen.

Debido a la naturaleza de este tipo de estudio, se adecua bien a enfermedades o desenlaces infrecuentes.

Lea También: La Validez de un Estudio De Investigación

Un estudio de casos y controles parte del desenlace (outcome):

Buscándose la exposición hacia atrás. Esto lleva a un diseño eficiente y práctico. Esta ganancia de eficiencia lleva inconvenientes, que algunas veces son difíciles de eludir, el principal es que el muestreo debe ser independiente de la exposición.

Es decir, la proporción de expuestos no debe verse sesgada en los casos y/o en los controles.

La selección de controles es uno de los aspectos críticos de este tipo de estudio. Para evitar sesgos, como primera medida, los controles deben seleccionarse de la misma base poblacional que los casos. Segundo, el tiempo-persona de cada control debe ser constante a través de todos los niveles de exposición.

Este segundo punto se puede contrarrestar seleccionando los casos al mismo tiempo que los controles (el mismo día o momento determinado de tiempo).

Por último, los factores de confusión deben ser contrarrestados en los controles, usualmente mediante análisis estadísticos.

Una de las estrategias para eludir la confusión es el pareamiento. Se realiza seleccionado los controles con base en una característica común en los casos, como la edad, el sexo, o el estrato socioeconómico.

Una desventaja es que en el escenario que se realice el pareamiento de una variable, se pierde información sobre esta en los controles, pues su medición va a corresponder a la información de los casos.

Además está el problema del sobrepareamiento, en el cual un estudio está emparejado por muchas variables; puede disminuir la validez interna y/o eficiencia del estudio.

Estudios de cohorte

Los estudios de cohorte bien diseñados son uno de los métodos pivote en la determinación de causalidad. Una cohorte se define como un grupo de personas con una característica definida hacia un desenlace, en este caso la característica es la exposición.

Este control de la exposición hace que uno de los criterios de causalidad sea fielmente investigado, el de la temporalidad.

A pesar de esto, la propiedad observacional del estudio, y la falta de asignación aleatoria de variables de confusión, hace que no se pueda establecer con certeza la causalidad.

Por este motivo, se han diseñado diferentes modelos matemáticos y métodos epidemiológicos para controlar la confusión.

Los estudios de cohorte pueden ser prospectivos o retrospectivos. Teniendo en cuenta que en los estudios retrospectivos se debe tener una información valida y completa de todas las variables de interés.

Esto es poco frecuente en países en desarrollo, y por eso en el contexto latinoamericano, generalmente estos estudios están reservados a poblaciones especiales, mayormente hospitalarias o de poca duración de seguimiento (pacientes maternas, por ejemplo).

En países europeos y asiáticos desarrollados, con cobertura de salud universal, los datos de todos los pacientes son guardados en grandes bases de datos que permiten el análisis poblacional retrospectivo de los mismos.

Pueden clasificarse como fijos o dinámicos.

Fijos cuando todos los individuos entran en el mismo momento del tiempo (el mismo día, por ejemplo), y dinámicos, cuando entran y salen a medida que pasa el tiempo de observación del estudio.

Un esquema simple de cómo se categorizan los pacientes y cómo se realiza el análisis en un estudio de cohortes se encuentra en la Figura 2. En los estudios de cohorte, como se miran solo los desenlaces nuevos, se estima la incidencia.

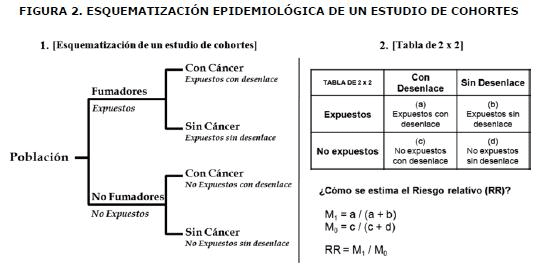
El indicador epidemiológico ya no es el OR, sino el riesgo relativo (RR), que va a estar dado por la incidencia del desenlace en el grupo de expuestos sobre la incidencia del desenlace en el grupo de no expuestos.

De esta manera (ver Figura 2; parte 2):
M1 = a / (a + b)
M0 = c / (c + d)

Donde M1 es la incidencia en el grupo de expuestos, y M0 la incidencia en el grupo de no expuestos. El riesgo relativo (RR), es la razón de las dos incidencias (M1/M0) (ver Figura 2; parte 2).

EL RR es la medida de asociación entre la exposición y el desenlace que se utiliza en los estudios de cohortes, y se interpreta de la misma forma que el OR.

Existen otras medidas de asociación que se utilizan en este tipo de estudio, pero analizarlas no está dentro de los objetivos de esta revisión.