Caos Determinista

DR. GUILLERMO SÁNCHEZ MEDINA

El Concepto del Caos

La palabra “caos” proviene del griego “kaos” que significa “abertura, o quedad, vacío, insondable”:

El latín “chaos” es la masa en estado bruto desordenado sin “caos” aparece también calificado por el adjetivo “determinista” y como una contradicción, cuando aparecen las dos palabras unidas caos y determinismo, sin embargo, lo que se entiende actualmente es un sistema determinado caótico como son los ya mencionados los atractores caóticos.

Por siglos o milenios atrás y aun en la mitología aparecen la idea de “caos en el universo” que necesita como una fuerza actuante del orden para luego pasar al desorden y así sucesiva­mente (ver mitos correspondientes obra “Ciencia Mitos y Dioses” y la “Teoría de la Comple­jidad”).

Por lo expuesto anteriormente se puede deducir que el caos pertenece a un sistema determinado con fuerzas, condiciones iniciales, situaciones respectivas las cuales son capaces de ser calculadas para encontrar una solución de conocimiento.

Lo general, dentro del concepto del caos se incluye la participación del azar (véase sistemas metereológicos). De una u otra manera en este concepto opera la necesidad y fuerza de razonamiento para cono­cer, describir los sistemas físicos que operan en el macro y micro universo y que nos llevan a entender el caos determinista.

Volviendo al término científico de “caos”:

Éste se refiere a un desorden y a una interco­nexión subyacente en que se manifiestan acontecimientos aparentemente aleatorios, pero con tendencias a la generación del orden, a partir del desorden impredescible, sin organización y por lo tanto con un comportamiento no determinista, no lineal, aparentemente no perió­dico (aperiódico) e inestable.

Aquí podría pensarse si en las ciencias exactas no se presenta la estabilidad, la periodicidad y el equilibrio; la respuesta es ambigua puesto que hoy día en las mismas matemáticas cabe lo “caótico”. ¿Cómo puede ser posible que del determinismo matemático se produzca aleatoriedades?; he aquí también el hecho de que el caos se presente cuando la complejidad aparece y la organización sistemática se disipa para llegar al cálculo de probabilidades, en un campo indeterminado.

Por lo tanto la respuesta sería afirmativa pues para enunciar la sola potencialidad de “espacio tiempo” en sus distintas escalas te­nemos que significar con un simple signo para simplificar todo el pensamiento abstracto y complejo; además ya se ha creado la nueva matemática y estadística compleja, más allá del campo euclidiano con ecuaciones no lineales, no predescibles, con múltiples variables, en un continuo; así ocurre también con la naturaleza de los sistemas neurocerebrales, endocrinos e inmunológicos genéticos que producen equilibrios (²⁴²) y desequilibrios con autoorganización y estructuras transitorias complejas y simples, a la vez que disipativas.

La ciencia trató hasta hace poco describir y entender todos los fenómenos naturales como hechos lineales prede­cibles; así se desconocía “las propiedades emergentes” de los sistemas biológicos que son complejos no lineales, y a la vez son mayores que las que les dieron origen (Ibídem).

La ciencia o teoría del caos se centra en los modelos subyacentes que aparecen ocultos, en los matices, en la sensibilidad de las cosas y en las “reglas” sobre cómo “lo impredecible conduce a lo nuevo” (Briggs y Peat, 1999).

Esta teoría intenta comprender los movimientos y los modelos complejos de todo tipo que entienden un “cambio del orden al desorden y al caos con sus diferentes clases de órdenes estables que devienen inestables produciendo turbulen­cias y/o vórtices con un aparente desorden”, y, que, al mismo tiempo opera un modelo sub­yacente y cambiante; es decir, es una secuencia de fenómenos que se interrelacionan los que son estudiados a distintas perspectivas, (op. cit. Briggs y Peat).

De ahí también que se hable del “caos determinista” para explicar muchos fenómenos que se suceden en la naturaleza y en experimentos controlados en laboratorio, caracterizados por tener un comportamiento que no todo puede ser descrito por leyes matemáticas sencillas. De ahí que se hable de fenómenos caóticos cuya evolución es esencialmente determinista, y, a la vez cómo del caos se determi­na el orden.

Aquí recordemos que dentro de las leyes de la naturaleza está el desorden y el orden, el caos y la organización; aquí hay que hacer énfasis a que el caos pertenece a la ley entrópica y por consecuencia al desorden ya mencionado. El caos es equivalente a la entropía. Este último concepto ya está planteado en otra parte.

Desde el punto de vista histórico como se menciona en otra parte, conocemos cómo los mitos cosmogónicos parten del abismo cósmico, del “Tehom” u “océano caótico”; palabra relacio­nada lingüísticamente “Tiamat” del Dragón Babilónico y de la palabra “Tohuwabohu”(²⁴³).

Cuando nos referimos a la palabra “determinismo” lo estamos haciendo a una causalidad que implica también un posible predecir el futuro de un sistema conocido en un momento dado y de las condiciones o elementos que la constituyen.

De aquí se parte también a las ecuaciones que se crean en la física para expresar leyes, equilibrios, procesos dinámicos, relaciones causales precisas y variables.

Si observamos cuidadosamente en las ciencias y profundizamos en ellas vamos a en­contrar mecanismos ocultos, los cuales, entre tantos otros, tenemos que manejar a través de formas estadísticas, cálculos promedios, principios de equiparación, conocimiento de partes y del todo; es así como llegamos de la molécula, a la partícula con su posición, velocidad, para tratar de obtener un conocimiento del orden; así llegamos a la concepción del macro-orden y el micro-orden como al macro caos y el micro caos, presentes en el universo en donde está presente la materia y energía oscuras y así las variables ocultas.

De una u otra manera, las ciencias a través del tiempo siempre tienen una tendencia a encontrar el orden más no sin pasar por las ciencias del desorden en donde existe una escala de fenómenos desordenados e irregulares que no pueden reducirse a forma oscura; de tal ma­nera, nos encontramos con el desorden escondido con un aparente orden real y, así también nos basamos en las leyes de los grandes números en las teorías de las matemáticas, las mate­máticas complejas, la intersección de leyes causales independientes en donde se encuentra la independencia del pasado y del futuro.

Sin embargo, hay quienes afirman que no existen seres casuales independientes en nuestro universo, por ejemplo, cuando un caminante citadino le cae una piedra en la cabeza y muere. Se interpreta que existe una fuerza de atracción sobre el objeto que lo va a matar dentro de todo un contexto fenomenológico, metereológico y de la realidad externa; esta es una forma simplista de interpretar el hecho complejo.

Aquí nos encontramos en una franja entre el determinismo y el azar, o acto fortuito y casual. Karl Popper se pronunció en este sentido diciendo que “no somos capaces de predecir resultados individuales en el lanzamiento de un dado para deducir; y, para predecir se necesitan leyes y condiciones iniciales; las reglas para tirar el dado correctamente están elegidas de forma que no podemos medir las condiciones iniciales, por lo tanto decimos que el proceso es alea­torio”, (K. Popper, 1971). Esta temática ya está planteada en capítulos anteriores.

Al autor de estos textos cuando los estaba elaborando, se encontró con la obra “Mente y cerebro” de A. Rosenblueth, 2004, quien se pronunció cómo las características mesurables (de los sistemas materiales, relativamente aislados cuando están en equilibrio), y el postulado del determinismo de causalidad coexisten, siempre y cuando se conozcan las condiciones de los elementos que la constituyen; el tiempo es una de las variables, y para la demostración y descripción lógica, utilizamos la herramienta clásica de la ecuación diferencial, la cual en su relación es válida y valida el momento, la posición y el movimiento, la velocidad y acelera­ción.

“Hoy en día se ha llegado a la conclusión de que una ley puramente determinista puede manifestarse por fenómenos totalmente aleatorios (pertenecientes al azar) debido al ca­rácter no lineal de las ecuaciones matemáticas que modelan el sistema físico.

Dado que estas ecuaciones no permiten una solución analítica exacta²⁴⁴, los científicos han tenido dificultades para construir teorías que permitan su predicción” (Schifter, I., 1996). Aún más, se ha pretendido explorar e identificar pautas de comportamiento indispensables en las que intervienen combinaciones de experimentos numéricos y de análisis matemático para llegar al concepto de comportamiento irregular e impredecible aunque determinista, de los siste­mas no lineales y de la transición de un comportamiento regular a uno caótico a través de la llamada ecuación logística.

Aquí nos enfrentamos al determinismo disfrazado de azar, y las rutas hacia el caos, y, como decía Borges, “la decisión final no existe, se ramifica en otras”, puesto que la duplicación pertenece al mecanismo de bifurcación en el cual la periodicidad es difícil de predecir, (Borges, JL., 1974).

En el estudio de las bifurcaciones periódicas de la “ecuación logística” graficadas en el estudio del caos; el mismo Poincaré en 1908 concluyó que: sobre las ecuaciones que descri­ben la evolución temporal de varios sistemas, “una causa muy pequeña que se nos escapa, determina un efecto notable que no podemos ver y decimos entonces que tal efecto se debe al azar, lo que equivale a que, pequeñas diferencias en las condiciones iniciales engendren mayores en el fenómeno final”; de ahí el dicho popular “lo que mal comienza mal acaba” (Poincaré, H., 1944).

Para los autores arriba citados, y así lo entiendo y comparto, el modelo de la complejidad y el caos, es extensible a lo psíquico y a lo social, y sometido al cambio constante; por ejem­plo, todos somos “la misma persona a través de los años pero substancialmente una nueva persona, y cada uno está interconectado con los otros sistemas de la naturaleza, de la socie­dad y del pensamiento que nos rodea”, (op. cit. Briggs y Peat).

Dentro de este pensamiento, el caos nace de los órdenes psicológicos y físicos que conocemos, y que se desordenan e interactúan unos con otros para crear alternativamente zonas de colapso.

Con esta teoría se hace una serie de juegos de números, por medio de la cual el matemático Benoit Mandelbrot formuló unas ecuaciones reiteradas para mostrar cómo el número que crece puede decrecer hasta cero; esto llevado a la topología produce límites y formas extrañas con toda clase de repeticiones impredecibles (fractales); “esa conducta extraña muestra que el caos y su orden paradójico yace oculto incluso dentro de los confines de la lógica matemática”.

Así se produ­ce un atractivo estético. Estas ideas se aplican a la medicina, a la economía, a las dinámicas sociales para entender cómo cambian las organizaciones; “el caos a su vez, está dejando de ser una teoría científica para devenir una metáfora cultural y social” (Op. cit. Briggs y Peat).

Aunque la temática antes expuesta ya fue traída en textos anteriores, sirvan estas ahora para tenerlas en cuenta y comprender la complejidad que acompaña al azar y al determinismo en la naturaleza, el sujeto y en la sociedad y en toda la evolución. Es así también como se conjugan la teoría del caos y complejidad con el que postulo el azar determinista.

Entiéndase que este concepto de complejidad y caos conlleva la aceptación de límites y los no límites de la incertidumbre y la contingencia, del recordar y el imaginar, así como las necesidades de predicción y certeza, de manipulación y control, la percepción de lo armóni­co, lo simétrico y de la asimetría, de lo que crece y muere. En suma estas “teorías de la com­plejidad y caos pueden contemplarse como una metáfora”, mas nos ayudan a salirnos de lo insignificante y nos lleva a los orígenes que emergen del caos.

Los autores arriba nombrados enuncian “siete leyes” como lecciones; la primera se refiere al “vórtice”, la segunda se refiere “al efecto mariposa y la influencia sutil”; la tercera al “seguir la corriente” y “dejarse ir”, ley de “la creatividad y la renovación”; la cuarta la de “explorar de lo simple a lo complejo”; la quinta, el observar la ley “de los fractales y la razón”; la sexta “vivir dentro del tiempo” la ley de los “risos fractales de la duración” y la séptima “volver a unirse con el todo”, ley de la corriente de una “nueva percepción”.

Todos estos conceptos conlleva a un epílogo con res­pecto a cómo en la información existe siempre algo ausente y un agujero “ciego en el centro”. Estas reflexiones sobre el caos llevan a una concepción global unitaria y a cierta ubicación topológica en “el uno”, y en “el todo” como punto de partida y de retorno en la concepción del universo. (Op. cit. Briggs y Peat)

Cuando enunciamos el concepto de complejidad debemos hacerlo también con lo opuesto el de la simplicidad, pues uno y otro son polaridades que interfuncionan en diferentes posi­bilidades y alternativas como dos caras inseparables, la una de la otra, puesto que se interre­lacionan de igual manera como concebimos las contradicciones; por ejemplo, cuando nos referimos a la complejidad y a la simplicidad, lo hacemos también a la ordenación dentro de la complejidad caótica; este fenómeno se visualiza en la complejidad de los fractales que se pueden construir en los ordenadores en forma semejante a los conjuntos de ecuaciones con una complejidad infinita del caos y un orden simple que los mantiene unidos.

Otro aspecto que debemos mencionar aquí, es cómo de la simplicidad se puede llegar al opuesto, a la complejidad y viceversa, alternándose intermitentemente; estos fenómenos lo observamos en la sociedad; por ejemplo, en las interrelaciones de las cotizaciones de bolsa que se interrelacionan con fenómenos socio-políticos y aún psicofísicos.

Dentro de todos es­tos procesos en que intervienen factores opuestos se presentan el nuevo equilibrio; por ejem­plo, el ritmo de crecimiento de la población que fluctúa impredesciblemente de un año a otro. Briggs y Peat mencionan cómo “en vez que el orden nazca del caos, el caos ha surgido de un orden regular”.

Otro ejemplo de estos fenómenos es cómo “un acto irracional y aún un sueño o una coincidencia desafortunada desafían el orden normal de nuestras vidas, exigiéndonos que prestemos más atención a los matices y a los modelos sutiles” (Op. cit. Briggs y Peat). Aquí debe incluirse el concepto de “azar determinista” ya explicitado.

Conocemos a través de los escritos cómo se originaron los mitos y el primero el de la cosmogonía en donde en primer lugar estaba las tinieblas, la ausencia de luz y luego la masa primigenia de aguas rodeadas de tinieblas con un océano “caótico en el abismo cósmico” (“Tehom”). Allí, en el mundo del agua apareció la tierra.

Por siglos atrás y aun en la mitología aparecen la idea de “caos en el universo” (²⁴⁵) Por lo expuesto anteriormente se puede deducir que el caos pertenece a un sistema determinado con fuerzas, condiciones iniciales, situaciones respectivas las cuales son capaces de ser calculadas para encontrar una solución de conocimiento.

Lo general, dentro del concepto del caos se incluye la participación del azar (²⁴⁶). De una u otra manera en este concepto participa la ne­cesidad y fuerza de razonamiento para conocer, describir los sistemas físicos que se realizan en el macro y micro universo y que nos lleva a entender el “caos determinista”.

Actualmente en el Siglo XXI no solamente nos valemos de los mitos para estudiar los orígenes, sino que echamos mano de las matemáticas para estudiar cómo emerge el caos en los fenómenos cuya evolución es inicialmente determinista y en el cual participa el desorden y la aperiodicidad ; es decir sin tiempo y de lo que denominamos “caos determinista”.

De tal manera, tratamos de establecer límites para predecir comportamientos físicos macro y microscópico con niveles de energía en los sistemas químico-físico-atómicos, con reacciones oscilatorias y que se relacionan obviamente con el sistema solar del cual provenimos a través de un proceso y fenómeno del desorden al orden.

A todas estas definir el concepto de desor­den no es fácil pues evoca un estado de confusión, irregularidades, lejos de las leyes funda­mentales pero que de todas formas pertenecen a la ley de la entropía y por consecuencia del desorden que de una u otra manera, llevan a un “orden escondido” o no develado.

Téngase en cuenta que el mundo matemático es ordenado y lo contrario hemos podido comprobar cómo el universo matemáticamente es desordenado con desórdenes y caos determinados; de ahí lo que denominamos “caos determinista”.

Platón delineó tres niveles de comprensión: el primero superior ideal, el segundo del or­den y el tercero del caos. Obviamente podríamos inferir que estos órdenes están determinados por una ley del universo con características mensurables de los sistemas materiales.

Es así de tal forma, como se puede llegar a determinar el principio de causalidad, entendiendo el origen del universo a través de la participación del caos y el orden en las partículas subatómicas en las cuales operan procesos dinámicos con variables causales precisas.

Cuando hacemos mención a la teoría cinética de la materia, lo hacemos también a los gases; está teoría desarrollada por J. Maxwell²⁴⁷ y perfeccionada por L. Boltzmann (²⁴⁸) que determina el volumen, la temperatura, la presión y se calculan estadísticamente; sin embargo, existe una incapacidad para predecir trayectorias individuales de átomos y de sus partículas constituyentes.

Téngase en cuenta que la estadística es una manera objetiva y subjetiva de analizar lo subjetivo y objetivo de la naturaleza, pues nos encontramos con los sistemas ya muy bien mencionados complejos, en donde interviene un gran número de partes imposibles de conocer cada una de ellas; y, por ello debemos recurrir a la estadística.

Es por esto que se vuelve el conocimiento indefinido más aún cuando opera el principio de Heisenberg ya men­cionado, y por lo tanto cualquier medida es siempre insegura.

Aquí es necesario tener en cuenta que el macro-orden de la naturaleza obviamente depen­de del micro orden y micro caos de los procesos íntimos de la materia energía, enfrentándonos de todas maneras a que nada surge de la nada pues todo pertenece a transformaciones del caos y desorden que pasan a un orden.

En este momento el lector se podría preguntar si ¿existe una ciencia del desorden y del caos?; pues parecería que todos los fenómenos provinieran del desorden, y aún a través del tiempo los fenómenos ordenados se toman desordenados irregu­lares y no pueden quedarse estáticos puesto que se llegaría a “un punto de movimiento cero” que no existe (en el universo conocido) sino en la virtualidad o como un supuesto teórico, pero que en él, de todas formas, participa la temporo-espacialidad (pasado, presente y futuro en el aquí, allá y más allá) y con ello el movimiento.

Cuando reflexionamos sobre lo postulado anteriormente nos encontramos con que si no existe el punto “cero” como supuesto teórico, tampoco podríamos afirmar que el ser huma­no es único en los supuestos universos conocidos, sino que existe la posibilidad de réplicas iguales, semejantes en alguna forma o sentido, pues materia-energía se repiten con sus parti­cularidades y órdenes de acuerdo a las condiciones existentes.

Aquí valdría la pena pregun­tarnos ¿qué es el hombre (H)? la respuesta simple no la podemos reducir a una ecuación: [H= (CMEI)v=(me)xmo + AD], en donde C=cuerpo, M=mente, EI= evolución e involución; v=vida; m=masa, e=energía, x=? incógnita (desconocida), mo=movimiento ordenado, AD =azar determinista.

Entonces al volver sobre ¿qué es el hombre? La respuesta es compleja porque todavía no la podemos responder con toda la exactitud matemática, más cuando existe la variable (X) incógnita potencia; y, por lo tanto la ecuación no es válida.

A todas estas el ser humano requiere puntos fijos para apoyarse en ellos y encontrar una certeza de la existencia y de la verdad; y, con ello aparece indefectiblemente la necesidad del principio de causalidad, así también la necesidad y el deseo de interrelacionar e interconectar series causales dependientes o independientes, aleatorias o en oposición al determinismo.

Sin embargo, aparece también la pregunta: ¿existen series independientes acausales? Cuando nos planteamos esta pregunta es porque no conocemos las causas, porque somos incapaces de ello o porque nos falta información para conseguirla; por ejemplo, conocemos la existencia de algunas cuantas galaxias y los sistemas intragalácticos mas no todos ellos y menos sus interfunciones y aún menos las relaciones e interrelaciones galácticas; solo sabemos que el universo está en expansión porque las galaxias tienen sus movimientos expansivos.

De una u otra manera, cuando el ser humano no encuentra explicación se vale del con­cepto del azar porque no somos capaces de predecir los resultados individuales o deducir predicciones, porque para hacerlo se necesitan leyes y condiciones con causas iniciales; por lo tanto, si no se disponen de leyes apropiadas, el modo científico de predecir se desborona y por eso decimos que estamos en un proceso aleatorio.

Así como hablamos de caos, desorden, orden, lo hicimos con el concepto de determinismo ya expuesto con anterioridad en varios capítulos para explicitar cómo se conoce la causa y el efecto, las características que son mesurables, la probabilidad o posibilidad de predecir; esto ocurre si se conocen ciertos datos o condiciones de elementos, obviamente con sus variables o la ausencia de ellas pero si con posibilidad de llevarla a ecuaciones diferenciales, lo cual nos permite una relación válida entre la posición de un móvil, su aceleración y velocidad o al menos la función de onda de la trayectoria del móvil o el desplazamiento del mismo.

Téngase en cuenta cómo las leyes puramente deterministas pueden manifestarse por fenó­menos totalmente aleatorios puesto que el carácter del elemento no lineal de las ecuaciones matemáticas que modelan el sistema físico no permiten una solución analítica exacta, para construir teorías que otorgan la predicción certera e identificar pautas con combinaciones de experimentos numéricos y análisis matemáticos exactos.

“El mismo modelo matemático exhibe un comportamiento que parece azaroso a pesar del hecho de que las ecuaciones que describen son enteramente deterministas” (Schifter I., 1996); por ejemplo, en el modelo de crecimiento poblacional los valores iniciales evolucionan en una población que puede alcan­zar un equilibrio; además porque participa la presencia de atractores con un número dado de interacciones cambiando la dinámica en forma notable y así aparecen bifurcaciones de orden que alternan valores, puesto que cada una se ramifica multiplicándose; “estos mecanismos de duplicación periódica han sido muy estudiados ya que representa una de las rutas hacia el caos y es común en muchos sistemas dinámicos reales”

Por lo tanto, aquí nos encontramos nuevamente en el campo no lineal, y con el compor­tamiento irregular e impredecible aunque determinista de los sistemas no lineales y por lo tanto con distintas variables. Es así como aparece el concepto del determinismo disfrazado de azar.

(Lea También: Determinismo, Complejidad, Sistemas Caóticos y la Teoría Ergódica)

Al mismo tiempo debemos tener en cuenta cómo participan los valores de constantes en el proceso de las bifurcaciones, así mismo como ocurre en que “cada secuencia de puntos que origina una línea se reproduce el modelo global de la que le antecede” (Schifter I., 1996). (Figura 24 y 25).

 

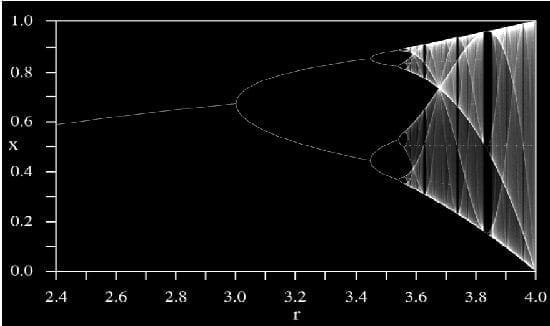
Figura 24. Diagrama de bifurcaciones de la ecuación logística cuando r varía de 3.5 a 4.  En el eje horizontal se encuentra el valor de r, en el vertical los de x. La teoría del caos probó que incluso sistemas realmente simple pueden resultar impredictibles con precisión en la práctica aún siendo deterministas. En la figura se muestra el diagrama de bifurcación para la aplicación logística cuya relación de recurrencia es simplemente \scriptstyle x_{n+1} = r x_n (1-x_n). Ref: Modificado de Schifter I., (1996). “Los mitos del caos” Fondo de Cultura Económica, México DF

Figura 25. Diagrama de bifurcación de la hoja de círculo. Regiones negro corresponden a las lenguas de Arnold. Ref: WP.

En el estudio del caos, Henrry Poincaré en 1908 se manifestó cómo: “una causa muy pequeña, que se nos escapa, determina un efecto notable que no podemos ver y decirnos entonces que tal efecto se debe al azar”; he aquí pequeñas diferencias que pueden operar en las condiciones iniciales y que engendran mayores fenómenos al final, parecido a la metáfora del fenómeno mariposa.

Aquí se me ocurre la siguiente idea: ¿qué podemos obtener si al hacer un electrocardiogra­ma, levantamos una gráfica exponencial y lo llevamos a ecuaciones numéricas? o, ¿podremos levantar una gráfica del movimiento de los planetas para conocer no solamente lo actual sino todo el pasado desde la creación del sistema solar y el futuro hasta su fin? Obviamente lle­vando estas gráficas a ecuaciones en este posible ejercicio ¿podríamos estar seguros de ellas?; habría que preguntarnos si estos sistemas permiten conocer las posiciones y velocidades en cualquier momento para llegar a un valor exacto.

Conocemos sí que los planetas se mueven alrededor de elipses y a su vez no todos los planetas tienen movimientos exactos, lo cual hace imposible la predicción; sin embargo, a los planetas Mercurio, Venus, Marte es posible pre­cisar su posición hasta 100 millones de años más con un margen de error de 0.00000001%. Esto se hizo gracias a las investigaciones de J. Laskar en Francia, (Laskar J.; Froeschlé C., 1991).

Dentro de estos conceptos del caos se incluyen los hallazgos de Eduard Lorenz quien calculó con tres ecuaciones diferenciales (tres ejes), las variables que representaban el mo­vimiento, la variación horizontal y vertical de la temperatura y encontró una manifestación de actividad exponencial debido a que corresponde a una evolución y a modificaciones de condiciones especiales; de ahí, el ya mencionado en otra parte, el fenómeno o efecto ma­riposa en el cual se muestra la modificación ampliada y/o duplicada cada tercer día, o 300 cada mes y 100 mil por cada dos meses para llegar a 1030 por año; por lo tanto los errores se multiplican hasta degradar la información de partida y obviamente la de llegada; y, así hace imposible la predicción de las condiciones o estados atmosféricos. De esto se concluye que las medidas que se determinan nunca son definidas; y, además cómo la dinámica del sistema caótico permite conocer nuevas informaciones que no se proyectaban o prevenían; he aquí también la intervención del azar en la que a la vez participa el cálculo de probabilidades y de lo que se denomina “sistemas azarosos”.

Téngase en cuenta que los matemáticos some­ten los resultados a pruebas estadísticas exhaustivas y así también encontramos los números aleatorios.

“Por lo tanto, según la definición técnica de caos, un sistema dinámico caótico es aquel que exhibe muchos de los atributos de los sistemas ideales aleatorios; … su evolución es impredecible debido a la extrema sensibilidad de las condiciones iniciales y el promedio de sus propiedades se puede escribir empleando métodos estadísticos” (Schifter I., 1996). He ahí la incapacidad de predecir la dinámica de los sistemas caóticos.

Cuando arriba nos referimos a la graficación, ésta conlleva la obtención de una forma geométrica progresiva de un estado dinámico según sus variables que lo caracterizan, y es así factible obtener gráficas simétricas o asimétricas con constantes e inconstantes o con fases, posiciones y velocidades distintas y aún fases en forma bi o tridimensional. Todo esto nos puede llevar a comprender topológicamente la dinámica lineal o compleja, en elipse o en espiral, con ciclos y límites de acuerdo a los elementos o sistemas que estamos graficando; también podemos obtener la magnificación del comportamiento en alguno de los ejes, todo lo cual se llevará también al cambio en el resultado de las ecuaciones.

Es aquí en donde se presentan los atractores fijos, periódicos y extraños en donde operan los sistemas, del orden y caos, el equilibrio y desequilibrio, las estructuras disipativas dentro de sistemas abiertos, en redes, bucles cerrados y la turbulencia (²⁴⁹).

En todos estos fenóme­nos participa “un determinismo” y al mismo tiempo “un azar”, así como un orden, un des­orden y un caos. La temática del caos también se desarrolla en otra parte. (Figura 26 y 27).

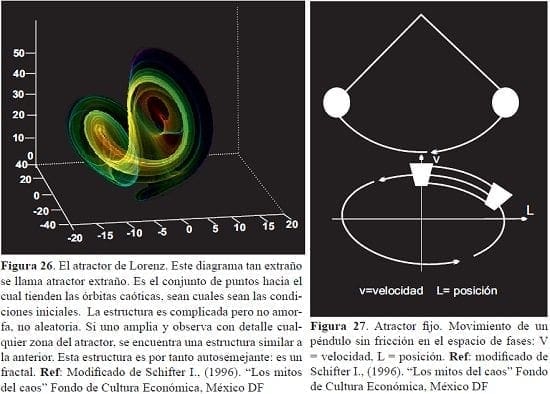
Los estudiosos de esta temática reúnen el comportamiento de la materia y energía, los sistemas mecánicos para llegar a la comprensión con modelos matemáticos y como ya se mencionó la graficación en tres ejes para determinar el comportamiento de los espacios fases, en los que operan los atractores (fijos, periódicos y extraños o caóticos) en donde aparece el concepto del caos. Parecería que el caos determinista es la fase anterior o posterior de la fase caótica completa en donde hay desorden; sin embargo, siempre hay límites témporo espaciales dentro del desorden, luego equivalen a que éstas variables de tiempo-espacio de­terminan el caos variante e invariante; por su parte el caos variante impredecible es la fase dentro del proceso caótico que producen conjuntos cíclicos.

Podría concebirse que no existen en la realidad cosmológica el caos permanente e in­variante, porque siempre está el límite y la ley del determinismo y del azar con múltiples transformaciones.

Cuando estudiamos el comportamiento de las estructuras de ciertas partículas podemos encontrar cierto predominio cíclico y geométrico; sin embargo con variaciones, y, a la vez, otras las más, que tienen un comportamiento caótico, desordenado en las cuales no podemos encontrar una linealidad o una secuencia y aún pliegues dentro de esas secuencias, sino un comportamiento completamente desordenado; sin embargo aquí podemos pensar si en ese comportamiento caótico determinista aparece una repetición.

Otro aspecto a dilucidar aquí es lo que conocemos como fractales en donde aparece el segmento del triángulo que observado microscópicamente termina en una curva límite espacial, formal con sucesión de puntos, y cada punto es curvo; he aquí también el espacio curvo repetido; he ahí también lo que se denomina “exponente de incertidumbre” que se calcula con la ecuación de Duffing (Aguir­regabiria, JM., 2010). (Figura 28).

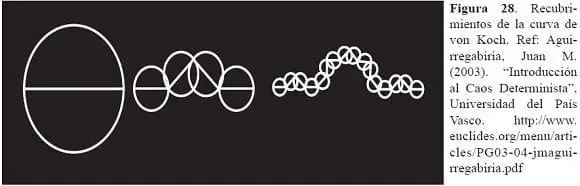
Todas estas conceptualizaciones las volcamos dentro de la física de partículas (²⁵⁰) y aún las llevamos a las mismas ciencias biológicas, pero también es factible hacerlo con las neu­rociencias y con ello al comportamiento del cerebro-mente con todas las variables del funcio­namiento neuronal y en esto los llamados potenciales eléctricos y bits cuánticos.

Por lo tanto en la teoría del caos, el comportamiento de los sistemas dinámicos es impre­decible y puede ser: estable, inestable y caótico; el primero tiende a un punto u órbita con su atractor, el segundo se escapa a los atractores y en el tercero caótico se puede manifestar en los dos anteriores; en estos sistemas se incluye la atmósfera terrestre, las placas tectónicas, el sistema solar y galáctico, el crecimiento de población y me atrevo a decir aquí, todo el sistema mental en que participa la imaginación con sus respectivas codificaciones.

Existe algo interesante, y es cómo se asimilan estos comportamientos en la dinámica cuántica y al funcionamiento neuropsíquico. Téngase en cuenta que las interpretaciones matemáticas, las físico-químico y cuánticas y las psíquico sociales, son diferentes, más los resultados seme­jantes con puntos de encuentros, anulación, sumación, exponencial, para llegar a un punto supuestamente inicial cero.

En síntesis y conclusión observamos que el desorden caótico tiene un determinismo y al mismo tiempo un posible “azar” con incertidumbre, y a la vez la dificultad o el obstá­culo de la predicción del comportamiento de las partículas.

Aquí viene la pregunta ¿entonces podríamos tener control del caos? ¿qué controla el caos en el universo? La respuesta muy posible se acerca a que es el determinismo del caos que controla todo ese proceso en donde opera la mecánica clásica y cuántica de los sistemas dinámicos y caóticos para llevar del caos al orden y de este al primero. Es posible que el cambio y control se establezca por estímulos energéticos que operan en un sentido u otro pero que conducen a la paradoja equilibrio-desequilibrio, orden-desorden.

---

242 El concepto de “equilibrio” no se puede referir a lo estático, estable, pues aunque existan equilibrios dinámicos, todo está en un cambio continuo; de ahí que podamos referirnos más a “equilibrios inestables dinámicos de transformación”, en el macro y microcosmos físico, químico, biológico, psicológico, social, económico, histórico-cultural.

Por su parte “un mundo o universo en un continuo equilibrio sería caótico”; lo que se sugiere aquí es que los cambios se organizan desde el punto cero (0) a todo lo conocido (energía-materia), y posiblemente a la inversa, con sus diferentes niveles y fronteras.

243 Lo que esto significa queda claro cuando Nietzsche utiliza precisamente el concepto de caos —que en realidad es un “no-concepto”, es decir, pone de manifiesto el carácter deficitario de los conceptos—para criti­car la insuficiencia y la ineficacia de interpretaciones como la del Génesis, cuando se dice que Dios es quien venció el “Tohuwabohu”, el “desorden y la turbulencia”, y a partir de él creó “todas las cosas”, todo lo que es y, en consecuencia, todo se dirige también a Él, (en “La verdad de la verdad”, de Wisser Richard, pág. 215 Universidad de Mainz) https://revistas.ucm.es/fsl/02112337/articulos/ASHF9393110209A.PDF

244 La negrilla es mía

245 Ver mitos correspondientes en la obra: “Ciencia, Mitos y Dioses” y “El psicoanálisis y la teoría de la complejidad” de G. Sánchez Medina.

246 Véase sistemas meteorológicos

247 James Clerk Maxwell (Edimburgo Escocia 1831, Cabrigde Inglaterra 1879) Físico escocés desarrollo la teoría electromagnética clásica; postuló la ecuación con su nombre demostrando que la electricidad y el magnetismo y hasta la luz son manifestaciones del mismo fenómeno (campo electromagnético). Su trabajo ha sido llamado segunda gran unificación en física y se le conoce por la estadística Maxwell Boltzman de la teoría cinética de gases.

248 Ludwing Boltzmann (Viena-Austria 1844, Duino Italia 1906) físico austriaco pionero de la mecánica esta­dística, autor de la constante de Boltzmann que reúne el concepto fundamental de la termodinámica.

249 Cuando nos referimos a “turbulencia”, en esta aparece la bifurcación, los espacios cambiantes y corrien­tes, los cambios de temperatura, velocidad y densidad, la mezcla de composición u homogeneidad de ele­mentos y así la incertidumbre. ¿Será la turbulencia una especie de orden disfrazado de caos?

250¿Cuál es el destino de las partículas elementales?

La respuesta es factible ubicarla en el comportamiento de las mismas o simplemente en la trayectoria, la cual depende de los atractores fijos, periódicos o extra­ños, produciéndose con ello los sistemas estables e inestables o caóticos, equilibrantes y desequilibrantes, simétricos o asimétricos, con bifurcaciones o estructura disipativas, fenómenos de auto organización, auto equilibrio, auto realimentación, retroalimentación, no lineabilidad, todo lo cual implica relaciones en todas las direcciones y el establecimiento de sistemas abiertos en red o bucles cerrados, que son aplicados al campo físico químico, psíquico y aún económico y social.

De ahí toda la complejidad en los diferentes campos; a la vez que sus consecuencias o destino en la confluencia o relaciones entre los sistemas integrados como son los del pensamiento, percepción, afectos, emociones y la conducta o comportamiento en general, o particular entre mezclándose con los productos de la imaginación consciente e inconsciente; todo ello con y en la par­ticipación del sistema consciente-inconsciente en la historia de la humanidad.