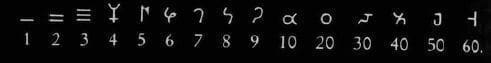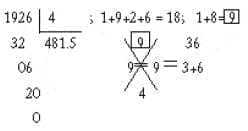La Numerología
El término numerología proviene de la palabra “número” y “logos o logía”, persona que se ocupa o cultiva la disciplina de los números; sin embargo, este término se refiere más comúnmente a una práctica adivinatoria o profética utilizando los números y conjuga el conjunto de creencias y tradiciones para la relación entre los números, los seres vivos y las fuerzas psíquicas espirituales; es más una pseudo ciencia.
En esta disciplina los números son conceptos humanos más perfectos y elevados y quien practica esta disciplina pretende investigar lo que denominan “vibración secreta” con códigos los cuales utilizan el número en su beneficio interpretando las influencias sobre las personas, cosas o eventos. Nótesele aquí como se le da una connotación de “vibración” (onda) con su adjetivo “secreto” (misterioso que no se conoce); además participa la interpretación dada por el sujeto a los hechos; lo cual significa que se le pone a los eventos lo que se cree o se quiere creer y se desea, por una necesidad.
Clases de numerología
Las clases se ubican de acuerdo a las escuelas, entre ellas están la cabalística, contenidos de la cábala; la caldea de la civilización babilónica y la egipcia; la China que otorga números con significados a diferentes formas; la pitagórica de Pitágoras la cual se guía por postulados del filósofo y matemático griego.
Los números (131)
Aquí viene una pregunta ¿cómo aparecieron los números? o ¿cómo se inventaron?, ¿cuál fue su historia? La respuesta es que el hombre por necesidad comenzó a numerar los objetos, a contarlos, y muy seguramente (no está comprobado) que utilizó las manos como ocurre en casi todos los seres que inician viendo y señalando al adulto, diciendo: “uno”, con un dedo, y luego el “dos” y así sucesivamente se fue contando con los dedos, primero en la primera mano y luego en la segunda, luego los dedos de los dos pies para llegar a 20.
¿Por qué usar las manos y pies? La respuesta posiblemente radica en que son prolongaciones corporales que 131 El ser humano creó, significó, simbolizó los números y figuras geométricas; a la vez que los denominó dándoles características significantes y representaciones con cualidades personales humanas; todo esto conlleva el mecanismos inconsciente de la identificación proyectiva que se pueden manejar fácilmente para llevar una cuenta; la palabra uno en los distintos idiomas obviamente significa la unidad; sin embargo, ¿cómo apareció la palabra dos y así sucesivamente?, ¿cómo contó el hombre de las cavernas y por qué? La respuesta era que tenían que captar los alimentos y darles unidades contándolos para saber la cantidad; así recolectaban lo que necesitaban y luego para intercambiar requerían saber cuánto tenían. Muy posiblemente surgió la necesidad de contar los astros, el sol, la luna y los astros más brillantes.
Figura 41. ¿Como se escribían los números?. Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
Muy posiblemente esto se fue organizando en el cerebro y el mismo cerebro hizo los cálculos contando diferentes unidades en principio, para llegar a los dedos de las dos manos (10) y luego de las manos del otro (otro 10) lo que equivale a 20 y así sucesivamente y también utilizando los dedos de los pies o se usaban las falanges de los dedos 6; la primera falange del dedo índice era uno, y cada falange era un número, por lo tanto el dedo meñique tenía las 3 últimas falanges y números 10, 11 y 12; luego cada dedo tendría 12 números para llegar a 60.. De la misma manera, utilizó a los objetos externos (personas, animales o cosas) dándoles números.
Aquí viene otra pregunta: ¿acaso en todo el planeta tierra apareció el conteo? La respuesta es que cazadores y recolectores llegaron a contar, algunos por ejemplo, la tribu “piraha” de la selva amazónica solo cuenta dos y los demás son muchos; en Tanzania la tribu “Asda” cuenta hasta tres.
Una interpretación que se le da para contar hasta diez fue por la necesidad de evitar los engaños; por ejemplo, cuántos peces sacaron o cuantos frutos. Obsérvese aquí que el engaño, el robo, la mentira, ya estuvo inicialmente desde ese entonces debido a las ambiciones y a las necesidades de la satisfacción oral (voracidad), para comer más.
La tribu Yupno de Papua Nueva Guinea cuenta sacos, fardos de hierba, cerdos, los días, las personas y los frutos.
Esta misma tribu tiene al menos 900 sistemas distintos de contar más allá de los dedos que tienen la base de diez. En algunas partes de esta tribu comienzan a contar desde el meñique y luego recorren la mano, el brazo, el cuerpo antes de pasar al otro y utilizan las palabras de esa parte para los números; por ejemplo, el número 14 es la nariz y para contar números mayores de 27 utilizan los hombros, lo que significaría que 40 sería un hombre y un ojo derecho.
Los babilonios que vivieron en Irak hace 5 mil años contaban a basa de 360 y llegaron a los 360 días del año contando los dedos; así mismo se inventaron los minutos y segundos.
La tribu Baruga de Papua Nueva Guinea, cuentan con 22 partes del cuerpo pero emplean la misma palabra dedo para los números 2, 3, 4, 19, 20 y 21, esto se hace para evitar confusión. Las manos son también útiles para la operación de multiplicar; por ejemplo, 7 x 9 se extienden las dos manos, se dobla el dedo número 7 y quedan 6 dedos a la izquierda y 3 a la derecha, (Kindersley, 2008).
¿Cómo se escribían los números?
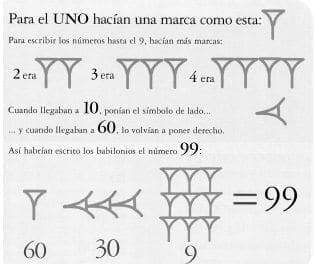
La respuesta es que hace 6 mil años cuando se contaba con las manos, los hombres aprendieron a domesticar animales y cultivar la tierra y pasaron de ganaderos a agricultores y así aprendió a comerciar en la compraventa y se guardaban registros con palos o marcas (en trozo de arcilla húmeda), o nudos de cuerda; así fue como se inició la escritura; por ejemplo, un óvalo podía representar un saco de trigo o una jarra o una tizana podía representar con su contenido la cantidad de líquidos, aceite, agua, miel, leche; más adelante vino la marca de las jarras o sacos, ánforas o botijos, dándole a cada una, una raya como símbolos las cuales se representaban con círculos y conos como las fichas antiguas; fue más adelante que vinieron las cuñas; por ejemplo, “uno” era una sola cuña y así el número dos, tres y cuatro hasta el número diez hasta que ponían el símbolo acostado y cuando llegaban a 60 volvían y lo ponían derecho, así llegó a sumar 99 de la siguiente forma: una cuña con el vértice hacia abajo y la base hacia arriba era 60, 30 eran tres acostados y nueve eran tres filas de tres hacia arriba lo que significaban 99.
Figura 42. Números babilónicos 4000-2000 a.C., Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
Los egipcios cultivaron la franja de tierra frente al rio Nilo que atraviesa el Sahara; años tras años se delimitaban los campos por la inundación del río, de ahí que se volvieran topógrafos y empleando las matemáticas para construir edificios; controlar el paso del tiempo de ahí viene la utilización de el pié como una medida y la yarda como el paso, la pulgada distancia de la falange del dedo gordo de la mano, el pelo como una unidad más pequeña, el palmo o el cúbito; el primero, distancia del dedo índice al gordo extendido, el segundo (palmo) el antebrazo y el tercero todo el brazo.
Los números egipcios no eran adecuados para realizar fracciones exactas, sin embargo, se las arreglaron por ejemplo para 1 cúbito estaba formado por 7 palmos, y un palmo constaba de 4 dígitos; sin las matemáticas las pirámides nunca se habrían construido; y, cuando llego el tiempo de los griegos obviamente ya estaban muy avanzados.
Los egipcios contaban en base de 10, y uno era una raya, 10 una curva hacia abajo y así sucesivamente véase figura 43.
Los números egipcios eran idóneos para sumar, restar, y no fácil para multiplicar. Sin embargo, se crearon trucos, por ejemplo multiplicar 13 x 23 se escriben en 2 columnas a la izquierda va el 1, 4 y el 8 y en la segunda el 23, 46, 92 y 184, entonces en la primera columna se suprime el 2 y en la segunda el 46 (lo que significa los números siguientes a los primeros) y luego se suma y nos da el primero 13 y el segundo nos da 299. Este sistema de sumar implica la multiplicación. (Kindersley, 2008).
Figura 43. Los egipcios contaban con base de 10, los números tenían forma de dibujos llamados ‘jeroglíficos’. Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
Figura 44. Los hindús utilizaban hojas de palma en donde escribían los números con tintas. Ref: Tomado de https://aprender-numeros.blogspot.com/2009_11_20_archive.html
Los babilonios 4000 a.C. señalaban al cero como un hueco o una cuña (el hueco de la cuña). Más adelante los griegos rechazaban al cero y aún Aristóteles lo consideró ilegal porque complicaba las operaciones. Los romanos no tenían un cero porque su sistema de cuentas no lo necesitaba y algunos pensaban que el uno no tenía sentido.
En el año 600 d.C., los hindúes inventaron el cero moderno y para ello utilizaban el círculo mostrando los huecos; sin embargo antes eran también el cero representado por el hueco que dejaba el guijarro en la arena. El cero llegó a Europa en el Siglo XII cuando los números hindúes aparecieron desde los países árabes hasta Europa y las personas pensaron que era más sencillo partir de cero en adelante.
Estos conocimientos llegaron al norte de África y América. Aquí es necesario hacer constar que el cero a la izquierda no significa nada sino está seguido de una coma que implicaría decimales y la derecha cada cero sería un múltiplo de 10, 100 y así sucesivamente. Las ecuaciones entre ceros no concluyen, por ejemplo 1 x 0 = 0 y así sucesivamente, (ibídem), (132).
Los números nativos americanos se contaban entre veintenas usando los dedos de los pies además de las manos; y, cuando se usaban granos de cacao, palos o conchas se agrupaban para formar hasta el número 20; para mayor de 20 se ordenaban los palos y granos en altura; en realidad el 0 para los mayas era significado por una concha. Para ellos no había sino que sumar los palos y piedras y cada altura para averiguar el número final, (ibídem).
Los número romanos se extendieron por toda Europa durante el imperio y se contaba por decenas y utilizando las letras para representar los números y aún podemos ver relojes con números romanos. Los números de 1 a 5 estaban representados por letras así: I, II, III, IV y V y así sucesivamente para llegar a 10=X, 50=L, 100 C, 500 D y 1000 M.; para los romanos multiplicar y dividir era complicado.
Los hindúes utilizaban el ábaco para el cálculo y se utilizaban cuatro filas; también se escribían los números sobre las hojas de palma en rayas; por ejemplo, el 3 eran tres rayas horizontales que luego se transformó al unirlas en 3. En realidad los números hindúes sustituyeron a los romanos especialmente en el renacimiento; y, un inglés llamado Abelardo de Bath (1100 d.C.) disfrazado de árabe tradujo la obra de Al khawarizmi y llevó el cero a la aritmética y así el logaritmo, (ibídem).
Existen múltiples ejercicios numéricos con los cuales el hombre puede jugar y alcanzar un cierto grado de magia (lo que equivale a que no se conoce) pero que existe; incluso soñamos con tener poderes mágicos.
Los primeros magos eran personas de tribus ancestrales que también se iniciaron con los juegos de los números, así se podía predecir estaciones, observando el sol, la luna, las estrellas, y aún se le dieron a los números la connotación de mágicos como “pi”, infinito, y números primos todo esto equivale a ciertos trucos y ordenamientos numéricos para realizar cálculos. Téngase en cuenta aquí, cómo los números fueron utilizados para medir el tiempo, el espacio y la cantidad de objetos clasificando unos y otros.
De la misma manera se hicieron cálculos con igualdades y sí también se podía predecir el resultado y también el cambio de estaciones, las distancias, se interrelacionaron hechos con los números y sus combinaciones para interpretar la buena o mala suerte.
Veamos algunos ejemplos que fueron sacados de “El taller de las tareas” Casa Editorial El Tiempo, 2008.
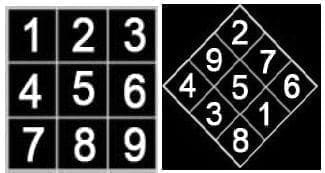
Figura 45. Cuadros mágicos. El más antiguo fue inventado por el emperador chino Yu el Grande hace 4.000 años. Ref: tomado de https://www.actiludis.com/?p=17930
El primer “cuadrado mágico” fue inventado por el emperador chino Yu, el grande, hace 4000 años utilizando los números del 1 al 9. Al escribir los números de izquierda a derecha en tres números consecutivos (1, 2, 3), (4, 5,6), (7, 8, 9) cualquier suma que se realice de arriba abajo o en cruz dan el mismo resultado.
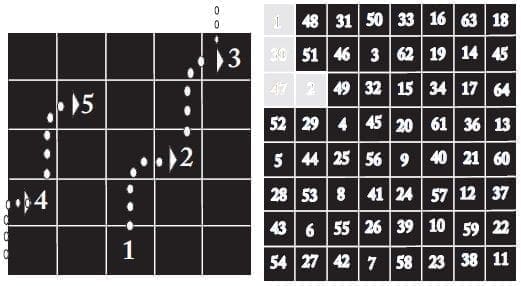
Otro es el que se realiza utilizando el paso del caballo en ajedrez. Se construyen cinco líneas de izquierda a derecha y de arriba abajo dejando un total de 25. Se inicia colocando el número 1 al azar; por ejemplo, en la fila inferior. Se cuentan dos casillas hacia arriba y una al lado como en el juego del ajedrez y así sucesivamente.
Cuando el caballo sale en el tablero vuelve a entrar por el lado opuesto y si el caballo no puede saltar dos casillas arriba salta dos a la derecha. Cuando está completo el cuadrado, los 25 números o un cuadrado de 8 horizontales y 8 verticales, se le da a los sujetos, ya con los números; la secuencia se puede construir de la misma manera. He aquí que no hay magia sino una construcción que el ser humano realiza en el ordenamiento de los números, (Kindersley, 2008).
La construcción del cuadrado mágico se hace ubicando números en 4 casillas sucesivas de arriba abajo y de izquierda a derecha, y la suma de estos números será supuestamente mágica por las igualdades en los resultados debido a la ordenación numérica para la suma de arriba abajo o viceversa, o de izquierda a derecha o viceversa, además de las diagonales centrales.
Figura 46. Cuadro mágico saltando como un caballo. Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
Leonardo Fibonacci de Pizza Italia hace 800 años (Siglo XIII) (133) descubrió una sucesión de números naturales o series la cual consistía en que se repetía el 1 y luego se sumaban estos dos para constituir el tercero; sumando el penúltimo y el último formaban el cuarto y así sucesivamente. Esto se llamó la matemática de “sucesión de Fibonacci” o la “serie de números de Fibonacci”.
Esta serie tiene una aplicación de las ciencias de la computación, las matemáticas y la teoría de los juegos y se encontró que aparecía en la naturaleza en las plantas, arboles y en la flora. Fibonacci escribió un trabajo sobre la sucesión de números descubierta por matemáticos hindúes como Pingala (200 a.C.), Gopala (1135 a.C.), Hemachandra (1150 a.C.). Todos ellos investigaron los patrones rítmicos que se formaban con sílabas o notas de uno o dos pulsos; el número de tales ritmos en cantidad de “n” pulsos producían o representaban la serie de Fibonacci. Esto mismo se aplicó a la solución del problema de la cría de conejo.
Figura 46a. Serie de números Fibonacci.
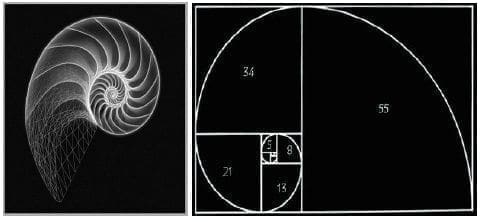
La sucesión de Fibonacci como se anunció anteriormente se realiza también en la naturaleza, en la genealogía de las abejas. En los pétalos de una flor también aparece la sucesión de Fibonacci: 3 pétalos, 5, 8, 13, 21, 34, 55 u 89 pétalos (como es el caso de las margaritas).
Esta sucesión se ha realizado en las novelas por ejemplo en el “Código Da Vinci” como una “ecuación de Dios” en la cual se supone que todo ya está enumerado y con ello predicho y por lo tanto se supone que todo está basado en la “ley del orden y caos” (134). En los números musicales también se ve este orden; por ejemplo, en el teclado de un piano se compone de 13 teclas sucesivas 8 blancas y 5 negras divididas a su vez en grupos de tres y dos para conseguir armonías.
Figura 47. La sucesión de Fibonacci es una secuencia de números enteros descubierta por matemáticos hindúes hacia el año 1135 y descrita por primera vez en Europa gracias a Fibonacci (Leonardo de Pisa). La Proporción Áurea (o Número Áureo, o Divina Proporción, entre otras denominaciones), es una curiosa relación matemática presente en la naturaleza: en las nervaduras de las hojas, en el grosor de las ramas, en el caparazón de moluscos, en las semillas de los girasoles, en los cuernos de las cabras, incluso en el cuerpo humano. Ref: https://numerosmorficos.blogspot.com/2011/06/sucesion-de-fibonacci.html
Fibonacci publicó el libro “Liber abacci” 1202 d.C.; Kepler a su vez describió los números de Fibonacci; y, Simson descubrió en 1753, la relación entre dos números de Fibonacci sucesivos los cuales se acercaban a lo que denominó Leonardo Da Vinci “proporción áurea”, la cual utilizó en sus cuadros. La sucesión de Fibonacci está relacionada con el número 1.618084 conocido como Phi.
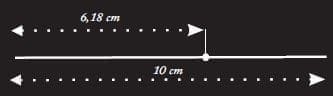
¿Qué es phi? Es el símbolo o representación de lo siguiente: se dibuja una línea recta de 10 cm de largo y una pequeña de 6.18 cm; la línea ha sido dividida en dos secciones; la división de la longitud de toda la línea entre la longitud de la sección larga se obtiene el número 1.618; y si se divide la sección larga entre la longitud de la sección corta, se obtendrá la misma proporción la cual es llamada, “proporción aurea” o Phi (φ); esta dimensión tiene propiedades extrañas puesto que multiplicando el número por sí mismo da el mismo resultado que si se le suma uno; si se divide cualquier número de la sucesión de Fibonacci entre la anterior se obtendrá una proporción cercana a phi; ésta aproximación a Phi, al avanzar a la sucesión, pero en realidad nunca llega.
En realidad es imposible escribir “phi” como proporción de dos números; es por esto que los matemáticos lo llaman “número racional”; este decimal puesto que nunca se acaban, (Kindersley, 2008) (135).
Figura 48. Proporción áurea, o phi, escrito φ. Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
¿Que tiene “phi” de mágico?, los antiguos griegos creían en la magia, puesto que aparecía en forma considerable sagrada; ésta consideración de “sagrado” es lo que le da el tono de mágico porque no se conoce. En una estrella de cinco puntas la proporción entre las líneas largas y cortas es exactamente “phi”.
Los artistas usaban “phi” y creían que las formas que contenían “phi” presentaban proporciones visuales completamente armónicas. Se cree que los arquitectos de la antigua Grecia utilizaron este concepto “phi” en los edificios; por ejemplo, en el Partenón de Atenas basado en rectángulos áureos. Téngase en cuenta que si se multiplica “phi por phi”, da “phi” más 1, o si se divide 1 a “phi” da “phi” menos 1.
Si bien los griegos fueron brillantes matemáticos también fueron especialistas en las formas, líneas, ángulos, la geometría plana y espacial, las cuales nos enseñan a diseñar y hacer cálculos utilizando las formas del cuadrado, rectángulo, rombo, trapecio, paralelogramo, romboide y calcular los arcos.
Parece que los cálculos sobre las distancias utilizando la circunferencia, la elipse, la parábola, la hipérbola fueron surgiendo en Asia Central, Mesopotamia y en Egipto para luego pasar a Grecia. En el año 1700 a.C. se escribió un rollo de papiro de 6 metros de largo con 85 problemas matemáticos y sus respuestas; en él aparecen las multiplicaciones repetidamente hechas por Ahmose quien fue el escriba que copiara el rollo sin embargo los autores se perdieron en el pasado.
En Grecia vivió Pitágoras (569-475 a.C.) el cual creyó que las matemáticas podían explicar todo; demostró que midiendo por la mitad la longitud de una cuerda musical se obtenía una nota más alta a la cual se le dio el nombre de “octava”; Pitágoras comprendió que la tierra era redonda y demostró el teorema sobre los triángulos rectángulos. El matemático griego Euclides escribió el texto denominado elementos y los utilizó para enseñar geometría lo cual duró 2000 años y demostró que hay un número infinito de números primos.
Kepler (1571-1630 d.C.) midió el recorrido de los planetas; Descartes (1596-1650) comprendió que había que utilizar 3 coordenadas para la dimensión del espacio y utilizó las letras del final, para representar valores del álgebra; Fermat (1601-1665) describió la prueba maravillosa de la ecuación xn + in = zn más no puede resolverse si “n” es mayor que 2; Pascal (1623-1662) a los 16 años inventó la máquina para calcular las ruedas dentadas; también trabajó en el problema del azar y estableció la teoría de la probabilidad y describió los patrones del triángulo; Newton (1643-1727) explicó la gravedad; Gauss (1777-1855) describió la ingeniosa forma de sumar números consecutivos rápidamente, y demostró que cualquier número es producto de primos (8= 2x2x2x2 ó 6 = 2×3).
Einstein (1879-1955) postuló que la luz tiene una velocidad constante y es atraída por la gravedad; y, que la masa y energía son versiones de la misma cosa. Una pequeña cantidad de masa (m) por la velocidad de la luz al cuadrado (v2=e o e=mv2) es igual a una inmensa cantidad de energía (e).
Nótese que en todos los nombrados no solamente existe un genio, un inventor, un calculista, sino el pensador que descubre el camino sencillo a través de la imaginación y, en todos existe un concepto que aparece como mágico cuando no se comprende.
Recuérdese aquí como el gran científico Galileo se pronunció así: “todo en el universo está escrito en el lenguaje de las matemáticas”. Es obvio que estas últimas nos han ayudado a descifrar secretos del universo y a medida que entendemos cada aspecto del mundo (tiempo-espacio) también lo hacemos con el arte hasta llegar a los conceptos filosóficos sin descuidar todo lo que nos aporta el color, el cual a la vez, también lo podemos conectar con las matemáticas en beneficio del hombre.
Esto último lo hemos podido observar recientemente en la naturaleza con las formas irregulares y conociendo los fractales de Benoit Mandrelbrot con los cuales se calcula los números imaginarios que nos lleva a un sinfín o variaciones infinitas. De todas maneras matemáticas, artes, ciencias, se conjugan; sin embargo, aparecen las desilusiones mágicas y los trucos, (Kindersley, 2008).
El secreto de los trucos utilizando las matemáticas es encontrar atajos o lo que se podía decir saltos para hacer cálculos inmediatos en forma mental; por ejemplo, sumar números grandes mentalmente es más fácil si redondeamos al decimal; por ejemplo, para sumar 36 + 29 se redondea el 29 a 30 y luego se resta 1; otro de los ejemplos fáciles por ejemplo es multiplicar 73 x 11, se multiplica por 10 y se suma 1.
Para averiguar si un número es divisible entre 3 se suma el múltiplo de 3; por ejemplo 192= 1 + 9 + 3 = 12 entonces 1 + 2 = 3 múltiplo de 3 ó un número es divisible entre 4 si los dos últimos dígitos son ceros, y, un número es divisible entre 5 si el último dígito es 5 o cero; un número es divisible entre 9 si todos los dígitos suman un múltiplo de 9; ejemplo: 201.915, sumándolos da 18 y éste es múltiplo de 9.
Un número es divisible entre 10 si el último dígito es 0. Para averiguar si un número es divisible por 11, el primero se resta del segundo, el resultado se le suma al tercer número y luego se resta al siguiente y así sucesivamente; por ejemplo: 35706; 3 -5 =-2 + 7 =5-0 =5+6 =11, (ibídem).
Otro asunto diferente es el concepto de “Pi” que resulta de la circunferencia de un círculo dividida por su diámetro da el número irracional 3.14159265…; lo extraño sobre “pi”, es que no se puede calcular con exactitud y no existe una proporción sencilla como 22 dividida 7, que sea exactamente igual a Pi.
Escribir el número completo es imposible puesto que los decimales nunca acaban. Los egipcios (2500 a.C.) calcularon que Pi era 16 al cuadrado dividido por 9 al cuadrado o 256 dividido por 81 lo que equivale a 3.16. El filósofo Arquímedes 250 a.C. dibujó 96 lados alrededor del círculo y llegó a la conclusión que Pi se sitúa entre 220 dividido en 70 y 223 dividió en 71.
En el siglo XVI Ludolph Van Ceulen calculó 35 decimales de Pi. El astrónomo inglés John Machin descubrió en 1706 una fórmula complicada para averiguar los primeros 10 decimales; el matemático inglés Williman Chap duró 15 años calculando 707 decimales de Pi y cometió un error en 528 y a partir de ahí todos estaban equivocados; Yasumasa Kanada de Tokio en 2004 calculó 1.24 millones decimales de “Pi” ayudado por un computador. Para qué sirve Pi? Sin este concepto de “Pi” no podríamos fabricar ruedas, comprender movimientos de planetas y hacer unos cálculos necesarios en la tecnología moderna, (Kindersley, 2008).
El número mágico 1089. Consiste en abrir un libro en la página 10, se cuentan 8 líneas hacia abajo y 9 palabras hacia la derecha. Se anota la novena palabra en un trozo de papel, luego se mete en un sobre y se pone en la mesa debajo del libro. Luego se le pide a un amigo que piense un número de tres dígitos y que lo escriba. Vale cualquier número siempre que el primero y el último dígito sean diferentes.
Se le dice al amigo que invierta el número y que luego reste el pequeño del grande. Por ejemplo: 863-368=495. A continuación, que inverta los dígitos del resultado y sume otra vez los dos números: 495+594=1089. Posteriormente se le dice que utilice los dos primeros números de la respuesta para elegir la página del libro. Debería emplear el tercer dígito para encontrar la línea y el último dígito para hallar la palabra. Luego se lee la palabra en voz alta. Por último se abre el sobre y la respuesta siempre será 1089.
Dominó mágico. Se elige una ficha de dominó al azar, sin mostrarla. Luego se multiplica uno de los dos números por 5, después se le suma 7, luego se multiplica por 2 y se le suma el otro número de la ficha. A la respuesta se le resta 14 para obtener un número de dos dígitos compuessto por los dos números de la ficha de dominó. De esta manera se puede averiguar cuál es la ficha de dominó.
Los números primos. Un número primo es un número entero que sólo es divisible por 1 y por sí mismo; por ejemplo el número 23; el 22 no lo es.
(Lea También: Propiedades Matemáticas del Número nueve (9))
Algunos matemáticos consideran a los números primos los bloques constructores de las matemáticas porque se pueden crear todos los otros números multiplicando primos, por ejemplo: 5 x 11 =55, 3x 5 x 5= 75, 3 x 13 =39, 13 x 17 =221. Lo que sí es de tener en cuenta es que no se puede confiar en un solo patrón porque parezca que se pueda continuar la secuencia que se hace; es por esto que los matemáticos siempre necesitan pruebas.
Existe un misterio sin resolver sobre los números primos el cual se refiere a la forma en que parecen surgir al azar, entre otros números, sin patrón alguno, a pesar que se trata de encontrar; la falta de patrón significa que los números primos deben buscarse uno por uno (136); por ejemplo, se realiza una tabla de izquierda a derecha de 1 a 10 y cada columna lleva 10 dígitos secuenciales.
El 1 que no es primo se suprime, luego los múltiplos de 2 se ubican y luego los múltiplos de 3 se hace lo mismo, y de la misma manera con los del 4 que pertenecen al 2, y luego los múltiplos del 5 y los del 7; los números que quedan en la tabla sombreados son los números primos.
Tabla 2. Tabla de los números primos, los cuales carecen de un patrón; por lo tanto hay que encontrarlos uno a uno. Ref: Tomado de: “El taller de las tareas”. Dorling Kindersley, (2008). Bogotá: Casa Editorial El Tiempo.
El más grande hallazgo de los número primos tiene 7.8 millones de dígitos. El número primo más grande que se conoce llenaría 20 libros. Multiplicar números primos es fácil más no dividirlo lo cual es casi imposible. En la naturaleza se utilizan este cálculo como protección; por ejemplo las cigarras pasan 13 o 17 años bajo tierra como larvas para luego transformarse en adultos (el 13 y 17 son números primos) y así pasa en otras secuencias biológicas.
¿Existen números mágicos? La respuesta es que lo mágico aparece cuando el ser humano se sorprende por una respuesta que no conoce; por ejemplo, veamos la tabla siguiente: Cuando se multiplica un número por sí mismo es el cuadrado de ese número; y, cuando se organizan u ordenan los números en forma triangular se terminan con una secuencia especial que se llaman los números triangulares; por ejemplo el 1, 3, 6, 10, 15 y así sucesivamente y combinándolos se puede formar cuadrados.
Un hecho curioso con respecto a los números triangulares es que se puede formar cualquier número entero sumando no más de 3 números triangulares; por ejemplo, 15 + 36 =51.
Al sumar no más de tres números triangulares se puede hallar la edad; esto fue demostrado hace 200 años por el matemático Karl Gauss (1777-1855). La edad de 40 años, por ejemplo sería la suma de los siguientes números triangulares: 1 + 3 + 36 =40; la edad de 86 años sería: 55 + 21 + 10 = 86 y así sucesivamente.
Figura 50. La tabla piramidal de números triangulares y/o triángulo de Pascal. Ref: Tomado de https://www.disfrutalasmatematicas.com/triangulo-pascal.html
Con todos los números se pueden hacer series de combinaciones y según el ordenamiento puede obtenerse alguna coincidencia (igualdad numérica), la cual puede interpretarse como mágica o científica; así fue cómo surgió el triángulo de Pascal, una pirámide de números obtenida sumando y así se realizan diferentes cálculos con diferentes patrones.
Para algunos, como ya se mencionó anteriormente, las matemáticas tienen una magia según se maneje. Veamos unos ejemplos aparecidos en la obra ya citada: “El taller de las tareas”.
Otro concepto más sobre los números es sobre el infinito en donde todos los números de la fantasía caben y siempre se puede sumar uno más; por lo tanto, no existe límite y éste “no límite”, es lo que llamamos infinito. Así mismo conseguimos el tiempo como un infinito o eternidad.
El símbolo para infinito es un ocho acostado (∞). Aquí podemos pensar que cualquier evento que ocurra en el ser humano en su existencia es uno más de los infinitos o finitos (cuando lo ubicamos como el último) que han ocurrido en el cosmos; y, si le sumamos, restamos, multiplicamos el infinito a un número, nos dará siempre “infinito”.
De ahí que las matemáticas sean infinitas, y aún más las mismas fantasías que el hombre puede realizar en su existencia pueden llevarlo a lo infinito mientras exista. Sin embargo existen clases de infinitos uno para las matemáticas, otro para lo contable o incontable, otro para el ser en su mundo psíquico y otro para el tiempo del ser en la existencia.
Dentro de toda esta concepción aparece la necesidad del ser humano de encontrar órdenes, cálculos para prevenir, proyectar, y el deseo de provocar algo favorable, placentero y satisfactorio para el ser humano en su vida.
Volviendo a la numerología, conociendo sus principios estos se pueden usar para realizar tablas alfanuméricas, poniendo números a las letras del alfabeto y así poner un número personal más la fecha de nacimiento del sujeto de acuerdo a su nombre que sumándolo y haciendo la prueba del nueve da un número que sería el asignado o el de su destino. Ejemplo:
Tabla 3. Valores numéricos de las letras. Tomado de la Enciclopedia “Ser integral. Tendencias milenarias”. Autores: Jimena Perry, Bernardo Rengifo; Editoras Eugenia Arce, Clara Inés Quintín. Grupo Editorial Norma, pág. 63, Colombia, 2003.
Tabla Alfanumérica
Fecha de nacimiento 27-11-1972 sería: números de la fecha de nacimiento:
2+7= 9; 1+1= 2; 1972= 1+9+7+2=19; 1+9=10; 1+0=1 entonces 9+2+1= 12; 1+2=3,
Nombre Claudia sería: números de la tabla alfanumérica: 3+3+1+3+4+9+1 = 24; 2+4=6 los números 3 y 6 corresponderían al destino
Otro ejemplo: 21-6-1959 sería: números de la fecha de nacimiento:
2+1 =3; 6=6; 1+9+5+9=24; 2+4=6; 3+6+6=15; 5+1=6
Nombre: Lya: números de la tabla alfanumérica: 3+7+1=11; 1+1=2
los números 6 y 2 corresponden al destino.
Sumando los dígitos y restando el número 9 nos da un número el cual sería el de su propio destino con la significación e interpretación que se le dé en forma subjetiva explicativa.
Prueba del nueve
La prueba del 9 fue descubierta por el obispo Hippolytos en el siglo III y fue empleada por los matemáticos hindúes en el siglo XII.
El número nueve en aritmética es un número cardinal, ordinal con su factorización o potencial; por ejemplo 3 al cuadrado cuya numeración romana es IX que pertenece al sistema binario 1001 y dexagesimal y que tiene propiedades matemáticas.
Figura 51. La prueba del nueve se utiliza para verificar, de una forma sencilla, si una operación de suma, sustracción, multiplicación o división, realizada a mano, ha dado un resultado erróneo. Ref: Tomado de https://eloviparo.wordpress.com/2009/05/29/prueba-del-9-para-la-multiplicacion/
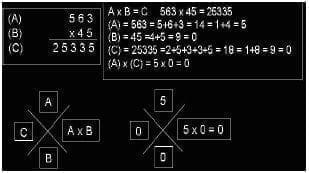
El 9 es el número natural que sigue al 8 y precede al 10. En la numeración romana se escribe IX, en la jónica θ. La prueba del nueve se denomina aquella que se utiliza para comprobar que una operación de multiplicación y/o división son exactas.
En la multiplicación se suman los números multiplicados, restándole el número nueve o dejándolo; lo mismo se hace con el multiplicador; el primero se pone arriba de una x y el segundo abajo del signo de multiplicación (x); luego se multiplicand uno por otro y al resultado se le resta el nueve y se ubica al lado izquierdo del signo x; finalmente se suma el producto de la multiplicación en la misma forma y el resultado debe ser el mismo aparecido a la izquierda.
Figura 51a. Otro ejemplo de la prueba del nueve.
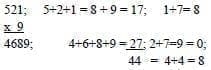
En la división se hace lo mismo con el dividendo y el divisor. La multiplicación de estos dos y su resultado debe ser el mismo de aquel producto de la división.
131 El ser humano creó, significó, simbolizó los números y figuras geométricas; a la vez que los denominó dándoles características significantes y representaciones con cualidades personales humanas; todo esto conlleva el mecanismos inconsciente de la identificación proyectiva que “incluye el deseo, la necesidad, el instinto y el objeto descrito por el psicoanálisis”, y por lo tanto con el soporte del pensamiento mágico omnipotente, de su historia y cultura; de ahí que el lector debe estar consciente de que cuando nos refiramos a la “significación” de los números, los postulados anteriores deben tenerse en cuenta, (GSM).
132 La graficación y significación de los números como ya se puede entender, se realizó con puntos, rayas, utilizando piedras, palos, círculos y objetos. Fue con el tiempo que aparecieron los números arábigos y románicos.
133 Su apodo era Fibonacci; vivió en Argelia en donde los árabes le enseñaron a utilizar los números hindúes, escribió sobre ellos y los popularizó en Italia.
134 Recuérdese aquí cómo los matemáticos y los magos vinieron de oriente (India, Asia Meridional, Caldea y Egipto).
135 Ver también el capítulo XVIII: “La terapia con geometría sagrada”.
136 Se contempla la igualdad en suma, multiplicación y división (son múltiplos cuando se pueden multiplicar, sumar o dividir porque el número mayor contiene al otro).
CLIC AQUÍ Y DÉJANOS TU COMENTARIO