Las Paradojas y el Azar Determinista

XI.

(Un juego de la lógica)

DR. GUILLERMO SÁNCHEZ MEDINA

Generalidades

Los lectores de estos textos habrán podido asumir que el “azar determinista” entra dentro del concepto de la “paradoja” como “una idea extraña u opuesta a la común opinión y al sentir de los hombres” o a la “aserción inverosímil o absurda que se presenta con apariencia de verdadera y que comprende una figura de pensamiento que consiste en emplear expre­siones o frases que envuelven contradicciones” (Diccionario de la Lengua).

La paradoja es una afirmación que parece falsa y en realidad es verdadera o viceversa, parece verdadera y es falsa, o pertenece a una cadena de razonamientos aparentemente impecables que condu­cen a contradicciones lógicas o una declaración cuya veracidad o falsedad es indecible.

Las paradojas también las encontramos en las matemáticas. Ppor ejemplo, en un conjunto infinito de elementos pueden ponerse en correspondencia biunívoca con los miembros de algún sub­conjunto dado. Aquí es importante tener en cuenta que es imposible establecer una correspon­dencia biunívoca.

De todas maneras, podemos aprender de las paradojas al igual que ocurre con los trucos del ilusionismo que nos causan asombro cuando son solamente manipulación de la sensopercepción.

Etimológicamente “paradoja” proviene del latin “paradoxa” y éste del griego παρά (para) que significa “junto a”, “al margen de”, “contra” por ejemplo paracionismo, parafrases, paradoja. Su significado ya fue enunciado en el párrafo anterior.

Cicerón consideró que lo que llamamos “paradoja” es una maravilla:

Y algo que parece asombroso y a la vez es una “anti­nomia” . Lo que significaría que la antinomia es una paradoja que engendra contradicciones y es una forma de razonamiento que en el caso particular de esta obra puede considerarse como una propuesta paradoja el “azar determinista”.

De lo anteriormente expuesto en la definición del diccionario se concluye que lo irracional y racional, lo lógico e ilógico se plasman en una idea, y, que en este caso es la que desarrollo en un análisis pormenorizado desde diferentes perspectivas.

Ejemplos de paradojas

Existen múltiples ejemplos, unos de tipo conceptual, de pensamientos, otros pertene­cientes a las ilusiones, otros a las matemáticas, algunos a las semánticas, así como a la teoría de la probabilidad. De una u otra manera, en las paradojas hay una combinación de ideas, figuras ambiguas, caligrafía, juego de palabras para crear una ambigüedad conceptual, visual o verbal.

La paradoja de Protágoras:

Sobre el “pleito de honorarios”. Protágoras de Abdera (485-411 a.C.) sofista griego recorría en su territorio cobrando elevadas tarifas por el uso correcto de la palabra. Platón lo considera como el inventor del papel del sofista profesional o profesor de virtud con la habilidad para tener éxito mundano.

La paradoja lógica se plantea entre Pro­tágoras y su discípulo Evatlo quien dice: “tanto como si gano como si pierdo en ningún caso tendré obligación de pagar a Protágoras.

Si gano el juez habrá desestimado la demanda, y si lo pierdo no habré ganado mi primer pleito y por lo tanto no se habrá cumplido la condición que hacía exigible la obligación de pago de los honorarios”.

Responde Protágoras: “tanto si gano como si pierdo este pleito Evatlo tendrá la obligación de pagarme puesto que si gano la demanda tendrá que pagarme pues esta es la cuestión que se ventila en este pleito, y si la pierdo también tendrá que pagarme porque significará que ha ganado su primer pleito. Es decir se habrá cumplido la condición de nuestro acuerdo”, (Suber P., 1990).

La paradoja del infinito:

Sse refiere a dos paradojas de Zenón quien fuera un pensador filó­sofo y poeta de nombre Zenofanes 570 a.C., y quien dijera que el universo es singular, eterno e incambiable: “el todo es uno”. Este filósofo se conoce a través de los textos de Platón, Aris­tóteles y Proclus.

Paradoja de Aquiles y la tortuga:

La paradoja es la relación de lo discreto con lo continuo con 40 argumentos y aquí entran la paradoja de Aquiles y la tortuga. Aquiles el héroe veloz permite a la lenta tortuga una ventaja en la carrera, y al observarla en su totalidad conceptual surge la noción que la tortuga siempre va más adelante.

La paradoja de la flecha:

Een que en su recorrido éste último puede ser medido en instantes que no se mueve. Los instantes son tiempos infinita­mente cortos en donde no aparece el movimiento, como en las imágenes del cine (una imagen queda congelada y si se le da el movimiento a la película la imagen se mueve).

Estas parado­jas se asemejan al principio de incertidumbre de Heisenberg ya expuesto en otras partes.

Otra de las paradojas es la de la lógica de Rusell:

Por ejemplo, “dos conjuntos infinitos son equipotentes (o tienen el mismo número cardinal), si existe una disyección (aplicación sobreyectiva e inyectiva) del uno sobre el otro. El cardinal de un conjunto es pues la exten­sión (el caso de los conjuntos infinitos se conecta con el concepto de número finito). Yy, la equipotencia es la extensión de la noción de igualdad”. No todos los conjuntos infinitos son “de igual tamaño” (pensar, por ejemplo, en los números naturales N y los números reales R), por consiguiente es posible establecer comparaciones entre ellos (ver figura 23, pág. 326).

Dentro de estas paradojas lógicas se encuentra el teorema de Cantor:

“Dado un conjunto C, existe siempre otro de mayor cardinalidad, que es el conjunto de sus partes, P, C. Es decir el conjunto de todos los conjuntos de C. La paradoja de Rusell es la contradicción entre el teorema antes mencionado de Cantor porque todo elemento de un conjunto es una cosa que está englobada en el todo, luego P (U) debe estar contenido en U que debe ser mayor o igual”, (Apostol T., 1977).

Existen las paradojas semánticas (la del mentiroso):

Por ejemplo se dice en la sentencia A: “lo que estoy diciendo ahora es falso”. Si A es verdad es falso y si es falso es verdad. ¿Es esto paradójico? Tenemos dos afirmaciones condicionales. Si A es verdad, entonces es falso porque se explicita que ahora lo es. Y segundo, si A es falso también es verdad porque lo estoy diciendo que eso es verdad. Lo que equivale a que cuando algo es falso no es verdad, y que todo lo que es verdad no es falso.

Todo este silogismo pertenece a un razonamiento llamado “consequientia milabilis”, lo que equivale a que “si algo implica su propia negación se puede inferir que es negación”. Sin embargo, existe el principio de “bivalencia” que dice de manera esquemática cómo toda sentencia es cierta o falsa. Sin embargo, ¿es todo principio de biva­lencia cierto? Las preguntas se expresan en sentencias pero “no toda pregunta es o bien cierta o bien falsa”. Por ejemplo, la sentencia: “hasta ahora has dejado de fumar, si tú nunca has fumado”. Luego la afirmación no es válida. (Macho Stadler, M., 2003)

Aquí podríamos pensar en la solución a esta paradoja aplicando la famosa jerarquía de Tarski en el cual “el concepto ordinario de verdad es incoherente” y debe ser rechazado y reemplazado por unos conceptos de verdad jerárquicamente ordenados y expresados en un lenguaje que evoluciona de manera natural (³⁷⁷).

Paradoja de la vagüedad:

En esta paradoja son clases de argumentos paradójicos que se derivan de límites indeterminados en la aplicación de los predicados envueltos. Esto se le atribuye al lógico Eubulides de Mileto en que hacía el siguiente razonamientos: “el hombre con capucha: ‘dices que conoces a tu hermano. Este hombre con la cabeza cubierta es tu her­mano y no lo conoces’”.

El hombre calvo: “describiría a un hombre con un pelo en la cabeza como calvo y a un hombre con dos pelos en la cabeza, y ¿si tiene tres?”. Un grano de arena no es un montón; si un grano de arena no es un montón, tampoco dos granos de arena son un montón y 999 granos de arena tampoco son un montón, por lo tanto 10.000 granos de arena tampoco son un montón.

He aquí algunas respuestas a estas paradojas. El lenguaje ideal es aquel en que se ma­nifiesta la precisión. Y, aparece la paradoja cuando se usa la vaguedad en el lenguaje. La utilización de lógicas multivalentes como la lógica difusa que sustituye a la usual con dos va­lencias, y reconoce para un objeto los grados de verdad. Por último la paradoja de “los granos de arena” es que “ninguna cantidad de granos hace un montón”. Lo cual es falso.

Otra paradoja es la de la predicción del condenado. 

En la edad media un rey pronuncia al sentencia ante un reo y le dice: “una mañana de este mes serás ejecutado, pero no lo sabrás hasta esa misma mañana de modo que cada noche te acostarás con la duda terrible de si esa será tu última sobre la tierra.

El condenado argumenta: si el mes tiene 30 días, no podré ser ajusticiado el día 30, ya que el 29 por la noche sabría que a la mañana siguiente abría de morir, así que el último día posible para cumplir la sentencia sería el 29, pero el 28 por la noche tendré la certeza de que por la mañana seré ejecutado. Y, así sucesivamente concluye que la ejecución es imposible y de ahí duerme aguardando que transcurra el mes para pedir su libertad. Sin embargo, el día 13 el verdugo con el hacha en la mano despierta al reo y más tarde lo decapita.

En donde ha fallado el razonamiento del prisionero. La respuesta radica en que no es lo mismo el día 30 más el día 29 más el día 28 etc., un conjunto es diferente y tiene distintas cualidades o propiedades. El ser humano tiene la cualidad de contener sorpresas”, (Op. cit, Macho M., 2003).

Hacía el Siglo III el filósofo chino Hui Tzu afirmaba: “un caballo bayo y una vaca parda son tres: el caballo, la vaca y el conjunto de caballo y vaca. He aquí la característica de dife­renciar conjuntos como el prisionero día por día y el filósofo unidad por unidad y el conjunto de la unidad”.

Existen distintas paradojas que aparecen en los textos y a través de los años.

Una de ellas se denomina la “fuerza irresistible” la cual es una paradoja clásica proveniente de la cultura popular China y que literalmente se denomina: “lanza escudo”. Esta paradoja proviene de una historia en la que “un traficante trataba de vender una lanza y un escudo al tiempo”.

Cuando le preguntaron cómo de buena era su lanza, él respondió que podría atravesar cual­quier escudo. Y, cuando le preguntaron cómo de bueno era el escudo, respondió, que podía detener cualquier lanza. Lluego le preguntaron qué pasaría si lanzaba su lanza contra su escu­do, el vendedor no pudo contestar, pues entró en una autocontradicción y así en la paradoja, pues una fuerza irresistible se oponía contra un objeto imperforable e inamovible.

El hijo del vendedor, rápidamente respondió: “depende de quien las use”. Aquí observamos la om­nipotencia ubicada en el objeto: “lanza y/o escudo”. La paradoja debe ser entendida como un ejercicio de la lógica y no como un postulado de una posible realidad. Een el caso de la “lanza escudo” están las “fuerzas irresistibles” de la lanza y el objeto inamovible del escudo; he ahí lo contradictorio opuesto y absurdo. La solución en este caso, no está en los objetos, sino en el sujeto (ser humano) que pone a funcionar con el “azar determinista”, los objetos.

Este tipo de paradojas llevaron al concepto de la “omnipotencia divina” cuando se pregun­tó:

“¿podría Dios crear una piedra tan grande que ni “El” mismo sería capaz de levantarla?” o “¿Dios puede autodestruirse?”. Aquí el juego de la lógica y de la ilógica con respecto a Dios de crear algo más grande que ni él pueda manejar con “fuerzas irresistibles”, objetos inamo­vibles, inercia infinita y masa infinita o quedar en la nada.

Por su parte una fuerza irresistible contiene una energía infinita, lo cual según la ecuación de A. Einstein de E= mc² implicaría también una masa infinita. Es como una bala de cañón que no puede ser absorbida y una pared que no puede ser derribada. Equivalen a un mismo tipo de objeto imposible, con una inercia infinita.

La paradoja de David y Goliat

Por su parte, lo infinito no tiene fin y no cabe la autodestrucción y la noche o la nada. Aasí se puede seguir con argumentos que nos puede llevar a incógnitas. Aquí se puede incluir la paradoja de David y Goliat: ¿qué hubiera ocurrido si el primero no actúa con su onda en la sien del segundo? Lo lógico es que el grande podía aniquilar al pequeño.

La “paradoja del cuervo”:

Propuesta por el filósofo alemán Karl Hempel (1940) en don­de la lógica inductiva desafía la inducción.

Se llama también la paradoja de la negación o paradoja de Hempel:

El ejemplo de Hempel es el siguiente (“principio de inducción”): “todos los cuervos son negros”. Si se examinan un millón de cuervos y “todos son negros” la conclusión es obvia. Más si a esta proposición hacemos otra como, “todas las cosas no negras no son cuervos”, entramos en un principio de inducción, más es algo contradictorio. Si todas las cosas no negras del universo, y si no hay cuervos entre ellas se podría concluir entonces que todos los cuervos son negros.

El ejemplo sólo se enfrenta a la inducción o deducción, por que el conjunto de cosas no negras están los cuervos. Dentro de este mismo pensamiento muy simplemente se llega a preguntarnos en nuestro propio racionamiento lo siguiente: si todos los “P” son “Q”, puede validarse que ningún P es Q. Eesto es de acuerdo a la simbolización o significación de P y Q. de todo esto nos surge que es un juego de la lógica, (J. L. Mackie, 1963).

Otra de las paradojas es la del “demonio de Maxwell”:

Se refiere a una criatura imaginaria ideada en 1867 por el físico escocés James Maxwell que hace parte de un experimento mental para ilustrar la segunda ley de la termodinámica, la cual se refiere a que entre dos cuerpos a diferentes temperaturas se puede transmitir el calor del cuerpo frío al cuerpo caliente, puesto que entra en el sistema aislado y la entropía nunca decrece.

La “paradoja estaría en que una criatura capaz de actuar a nivel molecular seleccionando moléculas calientes y frías separándolas, entraría a la selección y ordenación de moléculas, lo cual no es posible”.

Se denominó a esta paradoja el “demonio” por que proviene de un juego de cartas solitario en que se ordenan las cartas rojas y blancas análogamente a lo que se supuso en las moléculas calientes y frías.

“El hombre ordena las cartas”, más “no existe ningún ente que seleccione las moléculas calientes y frías”. Aquí viene una pregunta: ¿será que se podrá construir una máquina térmica capaz de seleccionar o mezclar las moléculas, violando las leyes de la termodinámica y teniendo la capacidad de decidir? La respuesta no es muy probable, puesto que aquí participa la capacidad de atracción y recepción y luego el acoplamiento para llegar a una equivalencia e isomorfía. De esto deducimos que la segunda ley de la termodinámica no puede violarse por sistemas microscópicos de información.

La disminución de la entropía, sin embargo, puede presentarse, pero a costa de gastar energía extraída de alimentos o de consumo. El ejemplo lo encontramos en la acción de determinadas enzimas, proteínas capaces de catalizar reacciones químicas en los organismos vivos y de reconocer sus materias primas y las acciones a desempeñar de acuerdo a las codificaciones en términos de información, en la propia secuencia de aminoácido de la proteína, (³⁷⁸).

Entre otras de las paradojas está “la de Galileo”:

Que es una “demostración de la propie­dad de conjuntos infinitos”. “El carácter paradójico se da por poner en entredicho el princi­pio de que el todo es el mayor de sus partes”³⁷⁹. Galileo hizo dos afirmaciones aparentemente contradictorias acerca de los números enteros positivos.

Primero “algunos números tienen la propiedad de ser un cuadrado perfecto (el cuadrado de un entero), mientras que otros no lo tienen”. “El conjunto de todos los números incluyendo tanto los cuadrados como los no cuadrados, tienen que ser mayor que el conjunto de los cuadrados”. Sin embargo, “por cada cuadrado hay exactamente un número que es su raíz cuadrada y por cada número hay exactamente un cuadrado”. Por lo tanto no puede haber más de un tipo que de otro. Este es uno de los primeros usos, aunque no el primero, de demostración a través de “una función biyectiva”³⁸⁰.

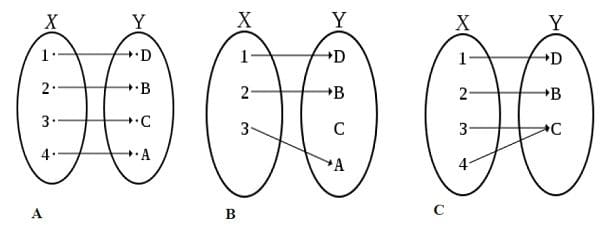
Figura 43. A. Funcion Biyectiva; B. Función Inyectiva; C. Función Sobreyectiva. Ref: tomado de https://es.wikipedia.org/wiki/Funci%C3%B3n_sobreyectiva

Cuando nos referimos a los números “pares” estos siempre podrán dividirse en 2, 4, etc. y nos darán un número entero (³⁸¹) positivo o negativo, y, si lo fraccionamos en 4 nos dará el cuadrado (por ejemplo, la división de dos (2) en cuatro (4), es 0.5 x 4 igual a 2, y si lo dividi­mos al dos (2) en dos (2) es uno (1) por dos (2) igual a dos (2); esto es obvio; sin embargo, si lo dividimos por un impar siempre el resultado será fraccionario; lo contrario, la división de impares 2 1, 3, 5, etc. Siempre nos dará impares y/o con sus fracciones, esto último implica la gran diferencia en el par e impar.

Galileo llegó a la conclusión de que “los conceptos de menor, igual y mayor sólo se aplica­ban a conjuntos finitos, y no tenían sentido aplicado a conjuntos infinitos”. En el Siglo XIX, Cantor, usando los mismos métodos, demostró que a pesar de que el resultado de Galileo era correcto, “sí se aplicaba a los números enteros o incluso a los racionales; la conclusión general no era cierta”; “algunos conjuntos infinitos son mayores que otros”; en el sentido en el que “no se pueden relacionar en una correspondencia uno a uno”, (³⁸²). He ahí el juego de la lógica.

Otra de las “paradojas es la de Olbers”.

Esta paradoja proviene del astrónomo alemán Heinrich Wilhelm Olbers que en 1823 formuló sobre el universo estático e infinito en el cielo nocturno debería ser brillante. Kepler en 1610 y Halley y Cheseaux por los años 1700 ya lo habían mencionado. El problema consiste en que “si suponemos un universo infinito, con un número infinito de estrellas luminosas, todas deberían terminar en una estrella y cada punto del cielo debería ser brillante, en un espacio uniformemente distribuido en el tiempo sin cambios radicales en la naturaleza de las estrellas durante el tiempo”.

Fue Kepler quien argumentó que en un universo finito, esto no es convincente, puesto que la luz de las estrellas es bloqueada o absorbida por el polvo o gas y sólo es observable a unas distancias finitas; además la recepción uniforme de radiación de todas las direcciones, no se observa, más cuan­do cada estrella contiene una cantidad finita de materia que sólo brilla en un periodo finito de tiempo; sin embargo, la paradoja está en que se supone que las estrellas se crean constante­mente en el universo, pero brillan en un periodo limitado de tiempo y luego desaparecen.

De todo esto concluimos que:

“Hay un número infinito de estrellas y también de objetos opacos (huecos negros) y el universo lleva existiendo una cantidad finita de tiempo con una finitud de estrellas”. He aquí la finitud del tiempo más aplicado a los objetos. De aquí el “problema de establecer la edad finita del universo de acuerdo a una evaluación matemática del hidróge­no”.

Por su parte conocemos que la cantidad de masa en las estrellas cuando es dividida por la cantidad total de masa en el universo es distinta a cero. De esto podemos concluir que en una unidad de tiempo, la cantidad de hidrógeno transformada en helio en una estrella cualquiera, divida por la masa de la estrella, es distinta a cero; además “no se conoce ningún proceso que pueda convertir un elemento más pesado en hidrógeno en la cantidad suficiente, y si existiese, seguramente violaría la segunda ley de la termodinámica; por lo tanto el tiempo necesario que las estrellas convierta todo el hidrógeno del universo en helio podría ser finito y no revertiría a su estado inicial” (Wesson P., 1991).

Paradoja de Heisenberg:

Esta paradoja también la denominamos de “incertidumbre o in­tedeterminación” y se refiere a que dos partículas no se pueden medir simultáneamente en la misma posición y velocidad; esta paradoja también puede relacionarse y/o asimilarse a la vida del ser humano, el cual se encuentra a cada paso con la incertidumbre, la indeterminación; y al mismo tiempo en el ser, éste no puede estar siempre en la misma posición y velocidad; esto es una mera analogía.

Paradoja de Mandelbrot:

Este científico fue quien sostuvo que las estrellas no tienen por que estar uniformemente distribuidas y la radiación cósmica de fondo es isotrópica hasta 1 x 10 mil. Por lo tanto la paradoja parte de una premisa falsa que en términos sencillos una cosa es el número de estrellas del universo indeterminado y otra cosa es el infinito postulado en el número de estrellas que son finitas o infinitas sin conocer la certeza.

Una paradoja apasionante es la llama la EPR:

(Por la sigla proveniente de los nom­bres Einstein, Podolsky y Rosen en 1953). Fue Einstein el de la idea que el entrelazamiento cuántico le resultaba perturbador por que las características de la mecánica cuántica si bien permiten concebir dos o más partículas, éstas no son calculadas al tiempo en espacio y veloci­dad y son imposible de obtener la información sobre el estado total del sistema y sólo podría calcularse la medición de una sola partícula; esta paradoja EPR está en contradicción con la teoría de la relatividad, ya que transmite información de forma instantánea entre las dos partículas.

En la paradoja EPR se conciben dos partículas que interactuaron en el pasado y quedan en un estado entrelazado. Si un observador mide el momento de una de ellas, sabe el de la otra; si mide la posición del entrelazamiento cuántico y obviamente en el principio de incertidum­bre de Heisenberg no se puede conocer la posición de la otra partícula en forma instantánea. De acuerdo a la paradoja, la teoría predice un fenómeno de acción a distancia instantánea pero no permite hacer predicciones deterministas; de ahí que la mecánica cuántica es una teoría incompleta. 

Esta paradoja es más una crítica que una paradoja, la cual se refiere a la no localización con posibilidad de acción a distancia y el problema de medición. Los procesos de medición en la mecánica cuántica obedecen a leyes deterministas. De todo este manejo de la física cuántica concluimos que la transmisión de información del estado cuántico entre partículas entrelazadas es lo esencial.

Dentro de las paradojas se encuentra una que se refiere al “fenómeno del pensamiento de grupo” por las teorías de conformidad con la psicología cognitiva, social que suele operar en los sujetos en su hablar, decidir y actuar.

Conocemos cómo un grupo puede hacer completamente lo contrario a lo que desea cuando uno de los pertenecientes por un motivo o un deseo de salir de una situación para plantear otra, no conforme con ella. Por ejemplo, trasladarse el grupo a otro sitio y el grupo interfunciona aceptando la sugerencia por creer que le da una satisfacción al otro y así sucesivamente; al final ninguno estuvo satisfecho. Esta paradoja se le denominó con el nombre de Aveline, pequeño sitio a donde un grupo se dirigió en esas circunstancias.

Existen otras paradojas en la geometría y en el cálculo que pertenecen a juegos de ilusio­nes ópticas y al de números de los cuales aquí no me ocuparé, solo traigo algunas imágenes que son utilizadas por la psicología cognitiva para mostrar la “gestal”.

Paradoja Psicoanalítica.

Los especialistas en psicoanálisis al leer estos textos muy bien pueden considerar que en la práctica psicoanalítica observamos la “paradoja del consciente e inconsciente”, de la “transferencia y contratransferencia, de las resistencias y contrarresis­tencias” y de toda una serie de mecanismos inconscientes que se manifiestan en las represen­taciones mentales o en sus derivados, en los sueños o en las conductas, acciones psíquicas paradójicas en que se ve la línea del deseo y la necesidad y sus contrarios del contra deseo y la represión a la necesidad.

Por ejemplo, el paciente acude al médico o psicólogo psicoanalista para ser tratado de una ansiedad fobia, convulsión, depresión, dolor, disociación, etc. u otros síntomas, por lo que manifiesta su deseo de mejorar o suprimir eso que le perturba o le duele; sin embargo hace inconscientemente todo lo contrario y lucha para el no cambio, puesto que el cambio significa pasar por estados de mayor ansiedad haciendo conciencia de representa­ciones o fantasías que son muy angustiantes o terroríficas y por lo tanto recurre a sus defen­sas.

Por lo tanto consciente e inconsciente siempre están presentes en el Yo del sujeto; más la paradoja no es de los contenidos (manifiesto y latente) estén ubicados al mismo tiempo en el consciente e inconsciente, sino que operan en forma opuesta desde su posición respectiva. Es por esto por lo que aquí denominamos “paradojas psicoanalíticas”; éste término que posi­blemente no es muy afortunado pero es la contradicción perenne que existe en el ser humano entre lo que se es, se piensa y se siente, (“se es y/o no se es”, “ser y no ser”). (^₃₈₃).

La paradoja de la “Gestalt”

Figura 44. La Gestalt. El término Gestalt proviene del alemán y fue introducido por primera vez por Christian von Ehrenfels. No tiene una traducción única, aunque se lo entiende general­mente como “forma”.

Sin embargo, también podría traducirse como “figura”, “configuración” e, incluso, “estructura” o “crea­ción”. En la figura se ve una capa (en negro) y dos siluetas en contraste en blanco; he ahí también la paradoja en las figuras y/o al mismo tiempo. La mente configura, a través de ciertas leyes, los elementos que llegan a ella a través de los canales sensoriales (percepción) o de la memoria (pensamiento, inteli­gencia y resolución de problemas).

En nuestra experiencia del medio ambiente, esta configuración tiene un carácter primario por sobre los elementos que la conforman, y la suma de estos últimos por sí solos no podría llevarnos, por tanto, a la com­prensión del funcionamiento mental. Este planteamiento se ilustra con el axioma: “El Todo Es Más Que La Suma De Sus Partes”, con el cual se ha identificado con mayor frecuencia a esta escuela psicológica. Ref: tomado de https://es.wikipedia.org/wiki/Psicolog%C3%ADa_de_la_Gestalt

Existe una paradoja, la paradoja de Fermi:

Que está condensada en la siguiente pregunta: “¿somos los seres humanos la única civilización avanzada en el universo?”; esta pregunta conlleva una serie de otras preguntas, a la vez que las dudas por la apertura de probabilidades en un universo tan inmenso.

De ahí que se sugiere entrar a ecuaciones para estimar el número de civilizaciones extraterrestres; más devienen otras preguntas y si las hay ¿dónde están?, ¿por qué no hemos encontrado ninguna evidencia?; ¿es nuestro conocimiento y nuestras ob­servaciones suficientes o defectuosas para confirmar lo positivo o lo negativo?; ¿acaso si son superiores a nuestra tecnología, por qué no hay señales de la misma?, y ¿si son inferiores será que alguna vez llegamos a conocerla?.

aquí otra pregunta perteneciente a la fantasía: ¿será que esas civilizaciones ya estuvieron en la tierra, dejaron sus huellas y se fueron?, o ¿será que vinieron se fueron y vienen de regreso?, ¿será que no nos conviene conocerlas?, o ¿será que ya están presentes en diferentes formas?, o finalmente ¿será que no existen?, ¿por qué los entes son tan distintos que la concepción de ellos no la podemos entender con nuestra tecnología?

Todas estas preguntas y sus respuestas llevaron a los científicos a la hipótesis de que la tierra es especial y que se refiere a que nuestro espacio está muy diferenciado, y aun al­gunos creen que es distinto dentro de toda la galaxia, (Vía Láctea), creándose así la conocida vida terrenal diferenciada obviamente de los planetas del sistema solar, y estableciendo que es muy improbable que existan todas las coincidencias y condiciones para la existencia de la vida como o igual a la vida terráquea.

¿Será esto cierto o sólo un supuesto explicativo por nuestra ignorancia?

Esta aseveración puede caer en el sesgo de la omnipotencia y exclusivi­dad del hombre en el universo. Los detractores de esta última afirmación niegan que puedan existir otras especies y otras formas de comunicación utilizando energías que por ahora no son bien conocidas.

También podría ocurrir que por el cálculo de probabilidades se consideren factibles otros lugares de nuestra galaxia, semejantes a nuestro planeta azul (punto azul en la galaxia co­nocida; sin embargo, ¿habrá más puntos azules?) del sistema solar y con ello la posibilidad de encontrar vida molecular, el ADN.

Si esto puede llegar a ser cierto; ¿por qué no hemos sido capaces de intercomunicarnos?; ¿será que nos falta tecnología, conocimiento y medios para ello o que la relación es un problema de tiempo semejante a lo que ocurrió con el des­cubrimiento de América?, ¿ Posible será que no están o estamos preparado para ello?.

¿será posible que las manera de transmitir información-señalización, y ellas mismas, son distin­tas pues pertenecen a otros códigos? Pensemos por ejemplo si los hinduistas y budistas,(³⁸⁴) que consideran la evolución y trasmigración de las almas o la reencarnación, ¿podrían estar planteando algo cierto del universo? La respuesta personal no la tengo, lo que sí es evidente es que en muchas creencias, las religiosas, desde milenios se considera “un más allá” de esta vida terrenal a donde viajaríamos todos en otra forma y dimensión (transformados en la esencia) para confundirnos o unirnos con el todo (fuerza unitaria, única que rige al universo).

Sin embargo, podemos seguir pensando que, ese más allá es la esperanza ante la nada.

Re­flexionemos cómo al colapsar la energía vital se detienen todos los procesos vitales y viene el proceso de descomposición celular, molecular quedando los átomos y partículas elementales que si bien no desaparecen si lo hacen en su organización vital (vida humana).

Entonces ¿esa energía atómica y cuántica se transforma y continua operando a otro nivel de organización? La respuesta no la tenemos como evidencia mas si en las elucubraciones que surgen de las representaciones proyectivas de los seres vivos, con sus funciones psicofísicas para pensar, imaginar, sentir y actuar.

Otro aspecto a considerar es que el hombre ha hecho en pocas centurias un salto científico y tecnológico para conocerse a sí mismo; sin embargo, nos falta recorrer mucho camino, más cuando sólo tenemos la capacidad del pensar, la inteligencia, para con ella hacer deducciones y conclusiones de las observaciones e investigaciones de todo del afuera limitado a nuestra percepción.

¿será que más acá y mas allá hay otra clase de conocimiento y otras formas, métodos de interrelación o de la citada comunicación lejos del pensamiento lógico objetivo, cognitivo, perceptual?

Sin menospreciar y/o demeritar lo existente y evidente permitámonos­los estimar e imaginar otros mundos, otras existencias y seres o entes diferentes a los otros; al hacerlo podemos ubicarnos en la franja de la concepción de algo inferior o superior, o distinto; así como en la tierra ocurrió la evolución de la vida, también puede haber, como ya se anotó otra clase de existencia. Las religiones lo aceptan y la misma ciencia es factible que lo acepte siempre y cuando lo demuestre con los conceptos de materia, antimateria, energía o función de onda y aún con las denominadas fuerzas ocultas demostradas su presencia con cálculos y ecuaciones matemáticas o a un solo con fenómenos o hechos derivados que por ahora o tienen explicación y solo existen descripción de ellos.

Al situarnos del otro lado de la galaxia o en otro rincón galáctico, ya nos estamos dando la posibilidad de viajar virtualmente, más no en la realidad, pues significaría nuestra propia des­integración.

Cuando imaginamos ese viaje y traslado lo hacemos con y como seres humanos en que nos acompaña la fabulación para evitar el dolor de la realidad. De tal manera, es sólo una proyección para satisfacer y llenar nuestra ignorancia y expectativa con nuestro propios deseos humanos. Más si imaginamos otro (s) algo (s) distinto (s), el científico realista obje­tivo nos catalogaría de fantaseadores, irracionales, fuera de la realidad terrestre, fronterizos y psicóticos con visos de ciencia ficción, o para otros en mejor de los casos espiritualistas, que buscan otras “casas” por la inconformidad que tenemos de estar, ser, hacer y tener en las que existimos.

He ahí también otra paradoja la del ser en este y otro mundo conocido y desconocido (³⁸⁵).

Existen críticos que se pronuncian en el sentido que aunque hemos estado buscando se­ñales extraterrestres por muchos años todavía no hemos oído ninguna emisora o radiación alienígena. A esta crítica se le pone la otra en que se dice que los extraterrestres pueden estar usando transmisiones por ondas no conocidas.

De todo esto podemos concluir que hay dos posiciones una que estamos solos y otra que estamos acompañados, una que el hombre no es el único y otra que es único e irrepetible, lo concreto es que no ha sido encontrada ninguna señal semejante a la nuestra. Aquí viene la pre­gunta: ¿será que la llegaremos a encontrar y si lo hacemos que va a ocurrir?, ¿será que puede acontecer semejante a lo pasado en el descubrimiento de América (ya los nativos americanos hacían alusión en sus mitos a la existencia de dioses venidos del oriente), o en tantos otros descubrimientos que los cuerpos estaban más no los medios de descubrirlos. (³⁸⁶)

Existe otra posición pragmática taxativa que es la que posiciona al hombre en el hoy y en la realidad de mostrar y se altera con la siguiente frase: no hay evidencia por ahora ni certeza de que existan seres semejantes o diferentes a los terrestres y lo que vale es lo que conocemos y no lo que suponemos, inferimos, imaginamos. Lo demás es entrar en la ciencia ficción la cual apasiona a muchos.

Estos postulados paradójicos con “hipótesis sobre la tierra especial”:

Tienen sus detracto­res a la vez los que utilizan ecuaciones y datos actuales para afirmar o criticar y contradecir. De una u otra manera existen principios contribuciones y aún postulados sobre la coloniza­ción extraterrestre afirmando la existencia de que los extraterrestres existían pero no lo sabe­mos todavía o estuvieron aquí pero no estábamos o que no se comunican con nosotros o no los oímos o han desaparecido, o no somos conscientes de ello, o nunca han existido o somos nosotros los únicos y los otros todavía no existen.

Lo que sí es una realidad es que el hombre está construyendo robots, hombres híbridos que podrán de alguna manera ser diferenciados en un futuro largo del hombre común y corriente, (³⁸⁷). Al mismo tiempo el ser humano traba­ja para buscar refugio en otro lugar o planeta en donde pueda subsistir, si la tierra se vuelve invivible. Recuérdese que ya existe la estación espacial y el deseo de viajar al espacio para encontrar otro lugar en nuestro universo.

¿Será todo esto de la presencia del terrestre y extraterrestre la gran paradoja con el azar y el determinismo que surge porque no aceptamos que solo los seres humanos somos una especie que apareció en la tierra con sus ciclos vitales como una gran oportunidad de tener conciencia y la capacidad de pensar dentro de la evolución natural para luego llegar a la in­volución volver a la nada o cero? La respuesta nadie la tiene por ahora, y como ya se expuso, las religiones si dan la esperanza y oportunidad de nuevas vidas, he aquí la incógnita y la curiosidad por el futuro.

(Lea También: La Paradoja “AD” El Azar Determinista de GSM y Penrose)

Aquí podemos incluir la paradoja del “gato de Schödinger” (³⁸⁸)

Otra paradoja es la de Newcomb (“new combination”, de nueva combinación).

Se trata de dos jugadores uno de los cuales puede predecir el futuro. Es paradoja por que lleva una contradicción, la causalidad inversa en que no puede haber libre albedrío en uno de los jugadores, puesto que aquel (libre albedrío) está definido en el problema del jugador casual que puede pronosticar y el otro no tiene verdadera elección.

Entre los dos participantes el que puede predecir ya está determinado y el otro sería el jugador normal. El juego se trata de dos cajas, una cerrada que contiene $1.000.000 ó $0 y el otro abierto $1.000. Los jugadores pue­den elegir entre la abierta que se conoce que tiene $1.000 o la cerrada que no se conoce cuánto tiene, pero el que vaticina ya sabe que tiene un millón. Las posibilidades de acertar no son equitativas, ni iguales y están determinadas por cierto conocimiento del que puede predecir, que le permite o no elegir. (Campbell, R., Lanning S., 1985; Levi, I. 1982).

Los filósofos en relación a esta paradoja comentan que “existen distintas probabilidades.

La primera, es que una persona racional escogerá ambas cajas o la caja abierta puesto que elige lo seguro que percibe, y una irracional sólo la cerrada”, lo cual concluiría que las personas irracionales podrían tener también una ventaja en el juego si aciertan en el azar. La segunda conclusión: las personas racionales tienen ventaja en el juego, ya que la predicción perfecta no puede existir. La tercera posibilidad se da cuando las predicciones son perfectas y la “casualidad puede invertirse”.

“Si una persona conoce realmente el futuro o lo que está presente y no se ve, y éste conocimiento afecta sus acciones, entonces los eventos en el futuro, causaran efectos en el pasado”. La elección del jugador será elección por la predicción. Una cuarta posibilidad es la que (si entramos en la máquina del tiempo) contemplamos las predic­ciones perfectas, “entonces no puede haber libre albedrío y el jugador escogerá lo que está destinado a escoger”.

La paradoja muestra que es imposible conocer o predecir el futuro.

¿Acaso de lo que se trata, como importante, es conocer el futuro?: ¿cuánto de él podemos vaticinar, prever o predecir?. ¿Será que podemos lograr con cálculos de probabilidades un alto grado de predicción? O ¿será que nos falta tiempo para alcanzar este conocimiento?, o por el contrario ¿será posible que ocurra lo mismo que acontece con el universo y sus fronteras que entre más alcanzamos a verlos y calcularlas más lejos estamos en lo incierto? Pienso que es mejor aceptar los límites y también renunciar a la omnisapiencia como otro deseo del orgullo del hombre en la tierra.

A este respecto Nozick (1969) en un escrito comenta: “Casi todo el mundo tiene claro lo que debe hacer” (conciencia moral). El problema consiste en que “la gente se divide casi a la mitad sobre cuál es la solución al problema, con un gran porcentaje que cree que la otra mitad está equivocada”.

Dentro de esta paradoja (Newcomb) el lector podrá observar que está la capacidad predictiva y dentro de ella la “intuitiva”, lo que implica es adelantarse (pre) al acontecimiento o a la percepción evidente. Aquí entramos nuevamente en el campo de la “percepción presensorial” inconsciente que obviamente no pasa por la consciencia.

Si a esto se le suma la perspectiva de la mecánica cuántica entramos en la incompatibilidad no solo del libre albedrío y la causalidad inversa, sino en esa otra percepción en la cual se puede realizar la elección. Sin embargo, queda la dualidad en el juego de las cajas con cero (0) o millones de pesos ($1.000.000) ¿está la caja llena o vacía en la realidad? Aquí entramos en el campo de probabilidades y al mismo tiempo en las capacidades inconscientes en donde existe o no existe la témporo-espacialidad conocida.

Aquí también penetramos en la teoría de los mundos paralelos, la cual lleva a la conclusión de que “tanto el libre albedrío como la casualidad son ilusiones creadas” por la correspondencia entre la consciencia y una memo­ria específica del flujo temporal y de las fuerzas de la mecánica cuántica.

Reflexionando sobre la paradoja de Newcomb se puede resaltar que es imposible o muy difícil conocer el futuro a nivel consciente y aquél (el futuro) “sólo es posible en casos en los que dicho conocimiento se vuelva consciente”.

A la vez la paradoja no tiene mucha consis­tencia debido a su propia contradicción sobre el supuesto conocimiento del futuro. De todo esto podemos concluir que no se puede maximizar sobre la predicción, el acierto, los vatici­nios, ni tampoco negar las capacidades sensoriales inconscientes, es decir, la presencia del inconsciente.

Las mismas matemáticas en una investigación que se hizo sobre esta paradoja encontraron que la escogencia de la caja cerrada se realizó en una proporción de 5 a 2 con aciertos del 71% vaticinando que el jugador escogería la caja cerrada. De esto concluimos que entramos nuevamente en el cálculo de probabilidades, a su vez por debajo de la predicción está la fuerza de la curiosidad, de descubrir lo que no se conoce.

---

377 Ver los conceptos de Verdadero y Falso capítulo V de esta obra.

378 Feynman, Richard P., Feynman Lectures on Computation (Perseus: 1996). Charles H. Hennett, “Demons, Engines and the Second Law”, Scientific American, pp. 108-116 (November, 1987).

379 Las negrillas son mías

380 Entiéndase nuevamente que la función equivale a la relación entre dos conjuntos en donde uno es el dominio y el otro el codominio. Cuando hablamos de función de correspondencia de conjuntos nos referimos a que cada elemento del primer conjunto se halla relacionado con un solo elemento del segundo, he aquí la función inyectiva, sobreyectiva y biyectiva, la última de ellas es cuando al mismo tiempo uno corresponde con otro, la primera inyectiva corresponde pero no sucesivamente y la sobreyectiva pueden corresponder dos en uno.

381 Los números enteros son los que representan las partes enteras de algo más o menos (+ ó -).

382 https://es.wikipedia.org/wiki/Paradoja_de_Galileo

383 Véase capítulo IX: “el ser y no ser”

384 “Para el budista el ‘viaje’ es la liberación del yugo del orgullo, que se obtiene saliendo de las vidas de la rueca e incorporándose a un nirvana espiritual, en los ‘mahometanos’ el ‘más allá’ es de naturaleza física”, (A. De Francisco, 2010).

385 “Los espiritualistas no expresan inconformidad por lo que tienen. O que buscan es demostrar la super­vivencia individual. En otros casos su deseo es poderse comunicar con seres de otros mundos y finalmente, logran el mejoramiento de sus espíritus”, (A. De Francisco, 2010).

386 “Según los mitos mesoamericanos el dios azteca, o mejor Tolteca, viene de oriente, (ya ha venido y volve­rá) (Quetacoatle)” (A. De Francisco, 2010).

387 Estos textos aparece en: https://es.wikipedia.org/wiki/

388 Ver la paradoja del “gato de Schödinger” al final del capítulo IV.