Una mujer de 45 años, que usted suele ver repetidamente, desde hace varios años, en su consultorio por una bronquitis crónica, acude en busca de su ayuda con su primera mamografía, tomada recientemente como tamizaje, en la que se reporta el siguiente resultado: “lesiones en la mama derecha sugestivas de carcinoma”.
Sin ambages la mujer le hace a usted una pregunta, que además es el centro del proceso diagnóstico en medicina: “estoy alarmada con el resultado de ésta mamografía, qué tan probable es que yo tenga realmente cáncer de seno” ?.
Los recuerdos al respecto, desde su época de estudiante de medicina, son los que la mamografía, para los propósitos de tamizaje, ostentaba una sensibilidad de 87% y una especificidad del 89%. 1 ,2 . Usted no es ginecólogo, mastólogo u oncólogo, pero de alguna manera tiene un compromiso implícito de, al menos, poderle brindar alguna información que disminuya la gran incertidumbre y preocupación de su paciente.
Para estar a tono con tan apremiante pregunta y en función de los propósitos pedagógicos del presente capítulo, es muy importante que no siga adelante sin haber seleccionado, dentro de las siguientes probabilidades expresadas en términos porcentuales, cuán probable es a su juicio, con los datos arriba mencionados, el diagnóstico de cáncer de mama en su paciente:
a. Menor del 25%.
b. Alrededor del 50%.
c. Alrededor del 75%.
d. Cercana al 100%.
(Lea también:Línea paraespinal, línea de unión posterior y banda traqueal posterior)
Jairo Echeverry Raad. M.D. MSc(c). EMJNC*
* Profesor Asociado, Departamento de Pediatría e Instituto de
Investigaciones Clínicas, Facultad de Medicina, Universidad
Nacional de Colombia.
Correspondencia: jecheverryr@unal.edu.co
Introducción
El proceso diagnóstico es el conjunto de técnicas, procedimientos y creatividades que permiten a un médico interpretar, de la manera más adecuada, la verdadera enfermedad que padece un individuo.
Durante su elaboración se desarrolla simultáneamente un menú de condiciones clínicas que pudiesen “encajar” con la problemática que se presenta, y a esto se le llama Diagnóstico Diferencial. Un Proceso Diagnóstico culmina habitualmente con un Diagnóstico, que es en esencia lo que el Médico cree que tiene su paciente. 3
La enfermedad, por otro lado, como lo habíamos señalado en capítulos anteriores4 , es la VERDAD, es lo que realmente tiene el paciente. A un individuo enfermo no le caben probabilidades de estarlo por cuanto la condición se encuentra de manera absoluta en él, sea que ésta se encuentre en su fase de inducción, de promoción asintomática o de expresión clínica.
Las personas están enfermas cuando “verdaderamente” lo están y no cuando tenemos las capacidades técnicas, tecnológicas o científicas de decírselos4.
Así las cosas, la Enfermedad va en un sentido (paciente –> médico) y el Diagnóstico en otro (médico –> paciente) 5 . El éxito de todo proceso diagnóstico, dados los diferentes sentidos, estriba en la coincidencia de éstos en algún punto.
El diagnóstico entonces es un verdadero problema para el médico de la misma manera como la enfermedad lo es para el paciente, y aunque no lo queramos, todo el ejercicio clínico se desarrolla con base en la solución de estos dos problemas.
El presente capítulo, pretende explorar los modelos que emplean los clínicos en el ejercicio cotidiano para aproximarse al diagnóstico, discutiendo sus fortalezas y debilidades y presentando, de una manera alternativa, la manera como esto es abordado por la epidemiología. Dada su naturaleza introductoria, aportaremos tangencialmente algunos conceptos, que serán tocados más a fondo en otros apartes de éste libro.
Elementos tradicionales para quién pudiera estar enfermo: propedéutica del proceso diagnóstico
La forma en que todos solucionamos los problemas diagnósticos es diferente, y valga decir inadecuadamente estudiada, sin embargo en el caso del ejercicio médico, ésta ha sido sugerida por algunos principios y técnicas de la semiología y la semiotecnia.
Hacer un diagnóstico tiene interesantes coincidencias con el proceso cognitivo humano6 . Se conocen algunos datos, se entienden, se analizan, se sintetizan y se resumen con el objeto de aplicar todo ello en la solución de problemas venideros.
El contacto inicial del médico y su paciente señala el comienzo de la actividad, a partir del cual se va surtiendo una historia clínica, con cientos de datos de su pasado y de su presente, contenidos en el motivo de consulta, la enfermedad actual, la anamnesis y el examen físico.
Algunos de éstos datos son referidos por el enfermo y otros son obtenidos e interpretados directamente por el médico, fruto de la observación y del proceso semiológico. A éstos les hemos llamado “hallazgos clínicos”.
Haciendo un breve paréntesis, ya que un proceso diagnóstico, en esencia, es la construcción creativa a partir de datos de diversas fuentes, calidades y características, la exactitud de un diagnóstico por lo tanto es inherente a la calidad de los datos obtenidos. La solidez de un diagnóstico descansa en la existencia de “datos ciertos”.
Dada la alta dependencia y sensibilidad entre la naturaleza de los datos y el diagnóstico derivado, y que el centro de todo ello en gran parte se construye a partir de habilidades de comunicación7 , semiología, semiotecnia y medición, se hace necesario destinar otro capítulo a la exploración de estos aspectos.
Proceso diagnóstico: recopilación y registro de datos
Continuando con el proceso, bajo una de las teorías cognitivas 6 ,8 se recopilan y registran en la mente todos los datos positivos obtenidos hasta ese momento. Algunos con un transcurso más elaborado reagrupan los datos en Síndromes clínicos, topográficos, pronósticos, etiológicos, etc.
En éste punto, hay varios métodos, formas o modelos distintos de razonamiento9 , los cuales son utilizados intercambiablemente por los clínicos de acuerdo a sus conocimientos y deseo: uno de ellos es un procesamiento absolutamente subjetivo en el que se sustenta el diagnóstico con base en la creatividad (heurística) llamado por algunos el modelo algorítmico, en el otro se intenta una mayor dosis de objetividad, el “anclaje implícito natural” llamado también el modelo lineal. La epidemiología propone en éste momento un modelo matemático, el razonamiento o modelo bayesiano.
En el modelo algorítmico, responsable de la construcción del Diagnóstico Diferencial, se utilizan aislada o simultáneamente dos técnicas, la repre- sentatividad y/o la disponibilidad.
En la representatividad 10 , el individuo compara y conecta el registro de datos obtenidos del paciente con conjuntos de datos que descansan en su memoria, agrupados bajo condiciones nosológicas, síndromes o mapas conceptuales.
Algunos expertos en pedagogía y psicología del aprendizaje llaman a esos datos los “insights” elaborados como reflejos de experiencias y conocimientos previos11 . La habilidad para derivar “insights” implica tanto capacidades de razonamiento y un desarrollo neurológico y cognitivo suficientes para soportar tal razonamiento, naturalmente variable de clínico a clínico.
El centro del interés es encontrar algún tipo de “resonancia cognitiva” entre lo que se está viendo en ese momento con lo que se ha conocido, vivido, o experimentado en ese campo (insights”), y es por lo tanto un nivel más elevado de elaboración mental que la simple adquisición del conocimiento crudo.
Diagnóstico diferencial
De ésta manera el diagnóstico diferencial es dependiente de cuán cerradamente los hallazgos que se encuentren en un paciente recuerdan otras condiciones que se conocen. De las capacidades memorísticas y naturalmente de la magnitud de lo que se conoció y se aprendió. En otras palabras del enciclopedismo y del razonamiento lógico.
La condición humana tiene una gran limitación en el volumen de lo que puede habitualmente relacionar, y le es difícil priorizar o estimar cuál de los términos “resonados” es el más cercano a la problemática que aqueja el paciente12 .
Si bien se han documentado multitud de sesgos al descansar el diagnóstico exclusivamente en la técnica representativa10, parece que el más protuberante es precisamente el determinado por la curva de aprendizaje, estableciéndose entonces pobres diagnósticos en individuos inexpertos y con poco tiempo de ilustración.
Anecdóticamente un valioso y reconocido internista, en sus etapas de entrenamiento, nos refería: “las personas están enfermas sólo de lo que yo sé”.
Disponibilidad: técnica creativa algorítmica
La otra técnica creativa algorítmica es la disponibilidad, en virtud de la cual el diagnóstico existe en función de la ocurrencia reciente, y por lo tanto aun fresca y disponible en la memoria, de un caso con manifestaciones similares aun cuando dicha condición sea infrecuente.
Esa capacidad de recuerdo es más intensa en la medida que el caso hubiese sido muy vívido, muy raro o que la condición pudiera entrañar grandes problemas para pacientes y clínicos. También se hace más disponible si la condición fue vivida o experimentada por un familiar o un relacionado.
Adolece de los mismos sesgos de la técnica representativa y es muy susceptible a presentarse en brotes epidémicos. Nuestra observación es la que los registros estadísticos de las enfermedades infrecuentes aumentan inusitadamente cuando dichas condiciones son objeto de revisión académica en las actividades hospitalarias como las reuniones clínico-patológicas.
Los médicos con cierta experiencia, que se surten fundamentalmente de las técnicas anteriores del modelo algorítmico, aprendieron además a interpretar para si mismos conspicuas “señales” de las enfermedades, elaboraron interesantes constructos en forma de “insights” mentales, y aunque no son objeto de análisis científicos, son a veces suficientes como valor agregado en su práctica dados los resultados significativos que a veces obtienen. Nosotros hemos hablado de que éstos médicos avezados tienen un magnífico “ojo clínico”.
Modelo lineal de anclaje y ajuste
El otro modelo diagnóstico un tanto más construido es el modelo lineal de anclaje y ajuste13 . Figura N 1. Bajo la perspectiva de éste, el clínico procede a “anclarse” en un punto inicial, en el continuo de probabilidad de enfermedad, y va sumando o restando de ese punto, de acuerdo al peso subjetivo de los resultados positivos o negativos, cambiando y fijando el ancla en otras posibilidades (moviéndola a derecha o izquierda según los resultados).
El cambio y nueva fijación a otras posibilidades es el llamado “ajuste” y ese nuevo ajuste es el nuevo Valor Predictivo, positivo o negativo, aportado por un nuevo dato. La decisión de descartar o confirmar un diagnóstico se basa en la suma “algebraica” de los pesos positivos o negativos de cada una de las pruebas obtenidas.

Figura 1. Proceso de anclaje y ajuste subjetivo de las probabilidades del paciente a las probabilidades de la enfermedad. En la medida que signos, síntomas o pruebas para-clínicas se vayan haciendo positivas o negativas, el “ancla” se moviliza a izquierda o derecha de la línea de ajuste de probabilidades.
Hay dos sesgos importantes de esta técnica y son la dificultad en establecer el punto de anclaje inicial (que usualmente se ubica en valores extremos), y la dificultad en determinar, según los nuevos hallazgos, en qué punto razonable se va a ajustar la nueva probabilidad.
En este modelo la velocidad y sentidos del ajuste están en función de dos elementos, el “peso” aportado por los datos encontrados y el “peso” del ancla. El “peso” del ancla, que es del resorte clínico, está construido con base en la experiencia acumulada y en algunas piezas aisladas de literatura científica revisada.
Punta del iceberg
Los que suelen practicar ésta técnica reconocen que, por su misma construcción y contenido, un Diagnóstico tan sólo está explorando la “punta visible del Iceberg” y no están total o absolutamente seguros de lo que están observando (con absoluta certidumbre).
En ese sentido también manejan el concepto de que a veces es mejor establecer la incertidumbre reinante y una manera de hacerlo explícita es con base en las probabilidades. Sin embargo esta técnica es aun subjetiva, frágil y pobremente reproducible.
El verdadero estado de un paciente descansa guardado en el interior de su cuerpo y no puede observarse directamente. El médico debe capturar una serie de datos externos imperfectos para deducir su real situación13.
Esto obliga, efectivamente, a hablar más en términos de probabilidades que de certezas. Si alguien verdaderamente sufre una enfermedad, su probabilidad de padecerla es absoluta, sin embargo, es posible que por la presentación, extensión o compromiso de ella, nosotros no estemos en capacidad sino de detectar una porción de dicha probabilidad.
La probabilidad diagnóstica que tiene cualquier individuo, es realmente las capacidades que se tienen hasta ese momento de diagnosticarle una circunstancia.
Epidemiología en el proceso diagnóstico
Tratándose del proceso diagnóstico, la epidemiología retoma la técnica del anclaje y ajuste, con igual sentido, y la surte de un razonamiento matemático, en el intento de reducir lo implícito, aumentar lo explícito, disminuir lo subjetivo, aumentar lo objetivo, reducir la variabilidad, aumentar la precisión, aumentar la reproducibilidad y mejorar la calidad del diagnóstico a través de un proceso sistemático.
Nótese que el razonamiento creativo en la construcción del diagnóstico diferencial es la pieza fundamental y no es excluyente del razonamiento matemático que se va a presentar y que es la propuesta epidemiológica del diagnóstico clínico.
Este razonamiento se fundamenta en un teorema fascinante. El de las probabilidades condicionales, que postuló el Reverendo Thomas Bayes (1702 -1761). De allí su nombre de modelo Bayesiano, en virtud del cual los médicos deberían cambiar sus creencias con respecto a un diagnóstico, de acuerdo al valor neto real que cada nueva pieza de información aporte al modelo.
Este razonamiento le permite al clínico con precisión y reproducibilidad calcular la probabilidad matemática exacta de un diagnóstico, que como veremos más adelante se denomina también probabilidad posprueba, y que para el ejemplo clínico inicial significaría, por ejemplo, el poder atrevernos a decir que la paciente de 45 años, hispana, con una mamografía positiva, tiene tan solo 0.94% de probabilidades diagnósticas de cáncer de mama.
Anecdóticamente, los familiares del Reverendo Bayes descubrieron éste fantástico aporte al conocimiento humano cuando estaban ordenando sus efectos personales tras su muerte1.
Pruebas diagnósticas igual a laboratorio clínico
Una concepción, inclusive en el cuerpo médico, es que una prueba diagnóstica es sólo aquella que se realiza en un laboratorio clínico, sala de Rayos X o en patología bajo el lente de un microscopio, y cuyo objetivo es confirmar la presencia de alguna condición o “explorar” qué está sucediendo con el paciente.
Sin embargo, bajo la perspectiva epidemiológica una prueba diagnostica es cualquier DATO que, obtenido a través de cualquiera de nuestros sentidos, de medios clínicos como la historia, el examen físico y los para-clínicos, modifique las probabilidades, ya en un sentido u otro, de asignarle a un paciente el padecer o estar libre de una condición3.
En medicina, cuando nosotros explicamos el significado de una observación, de un dato, nosotros decimos que “interpretamos” esa información y que estimamos la probabilidad de enfermedad, dada la presencia del hallazgo.
Ejercicio diagnóstico
El ejercicio diagnóstico se cultiva para detectar cada vez con mayor precisión y exactitud, indicios más precoces en los espectros preclínico, clínico y patológico de las enfermedades, y la clave en la interpretación de las pruebas diagnósticas es calcular a que probabilidad de la enfermedad corresponde el hallazgo clínico o para-clínico dado.
Aprender a hacer éstos cálculos requiere una breve excursión en la teoría de las probabilidades y en el modelo Bayesiano.
El solaz onírico que representa éste modelo para matemáticos y bioestadísticos, contrasta típicamente con las grandes dificultades en su entendimiento pero sobre todo en su aplicación por parte de nosotros2 , los clínicos, en y para lo que realmente debería servir, una ayuda para la solución de los problemas de nuestros pacientes.
Si Usted, como la gran mayoría de los médicos generales3 , fundamenta su proceso diagnóstico en los modelos algorítmico y lineal, conoce algo de la jerga asociada a las pruebas diagnósticas (sensibilidad, especificidad, valores predictivos) pero no sabe cómo utilizar pragmáticamente ello en la solución de problemas diagnósticos, tuvo que haber recurrido a una gran dosis de creatividad para seleccionar la respuesta a la escogencia múltiple del problema clínico inicial.
Tuvo que centrarse en la “gran” sensibilidad y especificidad de la mamografía y que, ya que el resultado fue positivo en su paciente, prácticamente esto le “asegura” la existencia de Cáncer de mama. Su conclusión, seguramente, fue que el diagnóstico era “muy probable” y asignó al menos un 75% de la probabilidad diagnóstica.
Si usted no se encuentra en éste contexto y es un cultor del razonamiento deductivo bayesiano, le hizo falta un elemento fundamental en la información suministrada, que por lo tanto le impidió o le dificultó hacer una estimación adecuada.
Modelo Bayesiano
Este es relativamente sencillo en su concepción y básicamente se resume en la combinación de varias probabilidades o riesgos. La probabilidad diagnóstica en un paciente se encuentra en función tanto del riesgo basal que tiene ese individuo de padecer la enfermedad como del resultado (positivo o negativo) obtenido de una prueba dada, que tiene valores determinados de sensibilidad y especificidad para esa enfermedad.
Aquellos interesados en la derivación de la fórmula matemática del teorema, pueden consultar el anexo correspondiente de éste libro u otras fuentes4 , 5 .
Los elementos consignados en cursiva en el párrafo anterior, requieren de cierta contextualización.
La probabilidad diagnóstica, la respuesta al problema diagnóstico en medicina, es una sentencia que tiene dos lados, o dos perspectivas diferentes del mismo fenómeno, analógicamente como lo fuese un vaso con agua que puede encontrarse simultáneamente “medio lleno” y “medio vacío”.
Si una mujer tiene definitivamente una probabilidad diagnóstica de tener Cáncer de Seno del 1%, tiene simultáneamente una probabilidad diagnóstica del 99% de no tenerlo. La primera debería llamarse, en honor a su verdadero significado, probabilidad diagnóstica positiva y la segunda probabilidad diagnóstica negativa.
Otras maneras más populares como son conocidas son el Valor Predictivo Positivo y el Valor Predictivo Negativo respectivamente. Figura 2.

Figura 2. Formato gráfico de la percepción del VAlor Predictivo, ya sea que se contemple la perspectiva positiva o negativa.
Es muy llamativo cómo, aunque en esencia son el mismo riesgo, pero explorado desde diferente perspectiva, los pacientes y aun nosotros mismos, interpretemos la información aportada dependiente del lado que se nos presente1.
Riesgo basal
El riesgo basal es la probabilidad del desorden de interés antes de que el resultado de una nueva prueba diagnóstica sea conocido2 o que se haya tomado una decisión clínica derivada de dicho valor. Otros sinónimos de éste termino son probabilidad pre-prueba, probabilidad ” pre-test”, riesgo pre-prueba.
La probabilidad pre-prueba, que en propiedad es otra prueba diagnóstica, depende de lo nutrido del contexto y del escenario en que sea contemplada.
Si un individuo es totalmente asintomático para alguna enfermedad, la probabilidad pre-prueba de “padecerla” (mas bien la probabilidad del diagnóstico de esa enfermedad en ese momento) es igual a la Prevalencia de la condición en la población (Prevalencia poblacional).
Si este fuese el caso, Usted necesitaría establecer en la paciente del problema que le consulta, cuál es la Prevalencia poblacional de Cáncer de mama en mujeres de 45 años del país donde se encuentre, y para ello son “vitales” las estadísticas vitales de los organismos sanitarios estatales.
Note cómo la probabilidad pre-prueba en éste caso se compone de cuatro pruebas diagnóstica separadas pero relacionadas: género, edad, país, sitio y nivel de atención.
Si el ejercicio fuese desarrollado en los Estados Unidos, la probabilidad pre-prueba de Cáncer de seno en ésta paciente sería del orden de 0.15% año3 (1.5 casos por cada 1000 mujeres dentro de los próximos 10 años), esto es, casi dos mujeres con cáncer de seno por cada 1000 mujeres de la misma edad y características.
Esta probabilidad cambiaría en la medida que cualquiera de las cuatro variables contempladas, fuesen modificadas.
Otros factores que afectan la pre-prueba
Hay naturalmente otros factores conocidos, aunque la mayoría aun no, que pueden y deben incrementar el valor de dicha probabilidad pre-prueba, que por lo tanto cumplen el criterio de ser pruebas diagnósticas y que sería menester contemplar. Como lo hemos reiterado 3,4 una Prueba Diagnóstica es cualquier dato que modifique los valores de una probabilidad de enfermedad en un individuo.
Se están construyendo afortunadamente elementos y recursos para el cálculo de probabilidades pre-prueba de las enfermedades prevalentes 4 ,5 ,6 pero el camino aun es incipiente.
Ampliando un poco más los datos de la historia clínica de nuestra paciente hispana, ella tuvo su primera menstruación a los 12 años, su primer parto de un hijo vivo a los 27 años, ni su madre ni sus hermanas han sido diagnosticadas con cáncer de seno, y no ha sido objeto de biopsias de mama.
Estos cinco datos nuevos (pruebas) deben modificar, en algún sentido, la prevalencia poblacional de 0.15% referida, y este nuevo valor es otra nueva probabilidad pos-prueba, que si no nos ayuda a tomar una decisión clínica, se convertirá nuevamente en una probabilidad pre-prueba en espera de nuevos datos.
Modelo predictivo
Si utilizamos el modelo predictivo7 , desarrollado a partir de los ensayos clínicos de la Iniciativa para la Salud de la Mujer8 (Women’s Health Initiative), podríamos definir, de alguna manera sobrestimada, que nuestra paciente tiene un riesgo de Cáncer de seno durante los próximos 5 años del 0.6%, o sea 0.12% de Prevalencia anual, asumiendo un riesgo uniforme a lo largo de ese tiempo.
Pues bien, si ha estado atento, ese es el dato primo, que necesita todo cultor del método Bayesiano para iniciar sus cálculos y fue la información faltante en la introducción del caso, sin la cual no se podría haber calculado adecuadamente la probabilidad pos-prueba.
Aunque suene ilógico si esta misma mujer, hubiese consultado en primera instancia a un especialista o a una institución especializada de tercer o cuarto nivel en el tema de Cáncer de mama, la probabilidad pre-prueba en ese sitio hubiese ascendido significativamente a cerca del 10%9 , más de 80 veces.
En tal situación, la mujer y su condición, tienen otras características y antecedentes que, de alguna manera, modificaron significativamente su probabilidad pre-prueba de enfermedad.
De la misma manera, el centro o individuo especializado a la que acude la mujer, se convierte en una prueba diagnóstica intensamente predictiva de la condición.
En virtud de lo anterior, todo clínico en ejercicio, que desee estimar válidamente sus probabilidades diagnósticas, debería medir y conocer la probabilidad pre-prueba de las condiciones con las que suele trajinar día a día, en los diferentes escenarios donde desarrolla su labor10 .
Datos en las pruebas diagnósticas
De nuevo, cada dato, que modifique en algún sentido las probabilidades diagnósticas de enfermedad en un individuo, es una prueba diagnóstica, pero cada dato observa el fenómeno desde diferente distancia3,9.
Es apenas natural, que en la medida en que el dato se encuentre observando la situación real más cerradamente, se tengan mejores capacidades para definir la verdadera situación subyacente, esto es, aumentar o disminuir mucho más las probabilidades en un momento dado.
Un dato muy fiel a la realidad, que siempre determina la presencia de la enfermedad cuando ella realmente existe, o por otro lado que no la encuentre cuando realmente no existe, generará intensas modificaciones en las probabilidades hasta los puntos en que confirmaría la presencia de enfermedad si el saliese positivo, o descartaría la misma si saliese negativo11.
Confirmar o descartar la enfermedad no es otra cosa que sobrepasar unos umbrales (unos valores en la escala de probabilidad) a partir de los cuales se está “suficientemente” seguro de la presencia o ausencia de la enfermedad12.
A partir de estos Usted no haría más pruebas y ofrecería un tratamiento o descartaría la enfermedad dado su resultado positivo o negativo respectivamente. Estos umbrales3, diagnóstico y terapéutico, serán explorados en otras secciones de este libro.
La distancia que separa cada dato de la verdadera condición, puede ser medida y establecida a través de sencillos indicadores, rotulados de manera genérica como rendimiento operativo de los datos o de las pruebas diagnósticas.
Una prueba diagnóstica es mejor en la medida en que ostente una mejor combinación de su rendimiento operativo. Los indicadores del rendimiento operativo de una prueba diagnóstica, contemplados de manera muy específica en medicina desde hace más de 50 años, son la Sensibilidad y la Especificidad13.
Sensibilidad o proporción de verdaderos positivos
La sensibilidad, también conocida como proporción de verdaderos positivos, es la capacidad que tiene una prueba de detectar los verdaderamente enfermos o con la condición bajo estudio, dentro de una población.
Esta capacidad se expresa en términos porcentuales con respecto a lo que, en las mismas condiciones, haría un patrón de referencia (estándar de oro). Si a una prueba diagnóstica no se le escapa ningún individuo verdaderamente enfermo, dentro de un grupo de individuos explorados, diremos que tiene una sensibilidad perfecta, equivalente a un valor de 100%.
De ésta manera, las pruebas con sensibilidad perfecta son las llamadas “tamizadoras” de las condiciones, ya que al no escapárseles ningún individuo enfermo, la presencia de un resultado negativo prácticamente descarta la enfermedad.
Como lo veremos en su momento, la verdadera utilidad de las pruebas de tamizaje, que ostentan sensibilidad total, es si ellas salen negativas por que descartan virtualmente la enfermedad.
Si a una prueba se le escapan algunas personas enfermas, comete errores por omisión. Y éstos se establecen cuantitativamente, como la cantidad que le hace falta a la sensibilidad para llegar al 100%. Esta cifra se le conoce como proporción de falsos negativos o proporción de escapes al diagnóstico.
Pruebas diagnósticas en cáncer de mama
La mamografía, como tamizaje, ostenta en las “manos” más experimentadas, una sensibilidad del 87%1,2, y por lo tanto una proporción de falsos negativos del 13%, lo que significa que de 100 mujeres que tienen cáncer de seno, sólo detecta 87 mujeres y se le escapan 13.
Trece mujeres con cáncer, que se pierden al diagnóstico oportuno, de cada 100 que lo tienen, son una cifra inaceptablemente alta y hacen de la mamografía, por lo tanto, una inadecuada prueba de tamizaje.
La falta de reducción significativa en las tasas de mortalidad por cáncer de seno, gracias a la implementación sistemática de programas de “tamizaje” con mamografía, se demostró de manera empírica14 y confirma de cierta manera la deficiencia técnica en éstos escenarios de la prueba.
Especificidad
La especificidad también se le conoce como proporción de verdaderos negativos. Es la capacidad que tiene una prueba de detectar solamente a los verdaderamente sanos o sin la condición bajo estudio, dentro de una población. Y ésta capacidad se expresa en términos porcentuales con respecto a lo que, en las mismas condiciones, haría un patrón de referencia (estándar de oro).
Si a una prueba diagnóstica no rotula equivocadamente a ningún sano como si estuviese enfermo, diremos que tiene una especificidad perfecta, equivalente a un valor de 100%.
Las pruebas con especificidad perfecta son las llamadas “confirmatorias”, ya que al no rotular falsa mente ningún individuo sano como si estuviese enfermo, un resultado positivo de la prueba prácticamente confirma la enfermedad.
La verdadera utilidad de las pruebas, que ostentan especificidad total, es si ellas salen positivas por que confirman enfermedad.
Si una prueba rotula individuos como enfermos cuando realmente son sanos, comete errores por exceso, y éstos se pueden establecer cuantitativamente, como la cantidad que le hace falta a la especificidad para llegar al 100%. Esta cifra se conoce como proporción de falsos positivos o proporción de excesos al diagnóstico.
La mamografía, ostenta paradójicamente una ligera mejor especificidad (89%) que sensibilidad (87%)1,2. La proporción de falsos positivos, por lo tanto es del 11%, lo que significa que de cada 100 mujeres sanas examinadas, la prueba asigna falsamente el diagnóstico de cáncer a 11.
Esta proporción de excesos, es la reconocida responsable de que un número importante de mujeres sanas sean objeto de futuras evaluaciones, innecesarias biopsias, ansiedad, costos y morbilidad derivada de ello15 . Se ha estimado que la realización de cuatro mamografías a una mujer, durante un período de 10 años, genera en ella un riesgo acumulado, de una mamografía falsamente positiva, cercana al 24%16 .
Para resumir
El rendimiento de una prueba diagnóstica se debate entre cuatro opciones: detectar los verdaderamente enfermos, detectar los verdaderamente sanos, escapársele verdaderos enfermos e imputarle el estar enfermos a individuos sanos.
El rendimiento operativo, establece el porcentaje de cada uno de estos aciertos y errores a través de la sensibilidad, especificidad, proporción de falsos negativos y proporción de falsos positivos.
Un paréntesis se hace necesario para decir que, si bien es probable que existan pruebas que muestren simultáneamente excelentes rendimientos tanto en la sensibilidad como en la especificidad, lo usual es que alguna de ellas prime, estableciéndose una especie de relación inversamente proporcional entre ellas y modificándose los valores de los cuatro elementos de su rendimiento.
A mayor sensibilidad de una prueba (y por ende menor proporción de falsos negativos) menor será su especificidad (y por lo tanto mayor su proporción de falsos positivos) y viceversa. Uno podría construir un listado separado de las pruebas más sensibles por un lado y las más específicas por el otro.
Una estrategia alternativa para la solución del problema
Retomando el problema y el contexto presentado, digamos que en nuestra paciente, después de tener en cuenta en ella cerca de nueve variables o datos (edad, género, raza, sitio, nivel de atención, edad de menarquia, edad del primer nacido vivo, antecedentes familiares de cáncer de seno y realización de biopsias de mama), hemos llegado a la estimación de una probabilidad basal (pretest) de cáncer de mama del 0.12%.
La paciente trae una mamografía, que ostenta una sensibilidad de 87% y una especificidad de 89%, la cual es reportada como positiva.
La pregunta en busca de espera sigue siendo la misma: “Dada la existencia de una probabilidad pre-prueba del 0.12% y una mamografía positiva (con 87% de sensibilidad, 13% de falsos negativos, 89% de especificidad y 11% de falsos positivos), qué tan probable es (probabilidad pos-prueba) que nuestra paciente realmente tenga cáncer de seno?”
De manera concisa, el método Bayesiano toma esos tres porcentajes y los inserta en una formulación matemática para establecer la respuesta. Existe creciente evidencia, que enseñar a estudiantes de medicina y a clínicos en ejercicio, el razonamiento Bayesiano en términos de probabilidades, no alcanza adecuado y sostenido aprendizaje con aplicaciones poco útiles en la práctica clínica17 .
Un método alternativo muy ingenioso, desarrollado por Gigerenzer y Hoffrage18 , sobrelleva estas dificultades. Ellos lograron demostrar, que el desempeño en la inferencia Bayesiana podría ser mejorada considerablemente al cambiar una parte importante del trabajo: LA REPRESENTACIÓN DE LA INFORMACIÓN19. Ellos proponen representar la información estadística en un formato que denominaron frecuencias naturales.
Nuestro problema expresado en frecuencias naturales sería así:
De 10.000 mujeres de 45 años, 12 podrían desarrollar cáncer de seno. Y, de esas 12 mujeres, 10 podrían recibir un resultado positivo de una mamografía para cáncer de mama. De las 9988 mujeres de 45 años que no desarrollan cáncer de mama, 1099 mujeres reciben un resultado de mamografía positivo para cáncer. Imagínese una nueva muestra de pacientes de 45 años que reciben un resultado de mamografía positivo: ¿Cuántas realmente tienen cáncer de seno?
¿Cómo encontramos esas frecuencias naturales y cómo le damos respuesta a la pregunta?.
Los pasos son los siguientes, que se grafican en la figura 3:
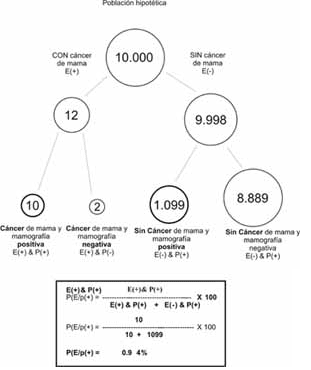
Figura 3. Representación de la información para la inferencia Bayesiana, mediante el formato de frecuencias naturales.
1. Seleccione una población hipotética suficientemente grande (p.ej. 10.000) y multiplique esa cifra por la probabilidad basal (pre-prueba) de cáncer de seno de la paciente. En nuestro caso 0.12% de 10.000 es 12 mujeres.
2. Tome ese resultado (12 mujeres) y use la sensibilidad de la prueba, para determinar cuántas mujeres tienen la enfermedad y la prueba positiva (87% de 12 es aproximadamente 10 mujeres).
3. Tome el número restante de personas que no están enfermas (9.988) y use la proporción de falsos positivos para determinar cuántos no están enfermos pero tienen la prueba positiva (11% de 9988 es aproximadamente 1099).
4. Compare el número obtenido del paso 2 con la suma de los pasos 2 y 3, para determinar cuántas mujeres con mamografías positivas realmente están enfermas mediante la siguiente ecuación:
P(E/p(+)) =((E(+) & P(+))/(E(+) & P(+)) + (E(-) & P(+)) )* 100
Donde P(E/p(+))es la probabilidad de cáncer dado un resultado de la mamografía positivo (probabilidad pos-prueba), E(+) & P(+), son las mujeres con cáncer y mamografía positiva (producto de la sensibilidad por la probabilidad pre-prueba), y E(-) & P(+) son las mujeres sin cáncer pero con mamografía positiva (producto de la probabilidad pre-prueba de no estar enfermo por la proporción de falsos positivos).
Como se aprecia en nuestro ejemplo, 10 mujeres de cada 1.109 tienen cáncer de seno (menos de 1% de probabilidad pos-prueba), cifra bastante distante de la que cualquiera hubiese podido calcular con métodos exclusivamente creativos.
Para concluir, diremos entonces, que en mujeres de 45 años con los antecedentes enunciados, y con una probabilidad pre-prueba del 0.12%, la presencia de una mamografía positiva incrementó su probabilidad, ahora probabilidad pos-prueba, a casi un 1% (exactamente 0.9%).
Convenciones
E(+): Enfermedad presente, E(-): Enfermedad ausente, P(+): Prueba positiva, P(-): Prueba Negativa. P(E/p(+)):Probabilidad de enfermedad dada una prueba positiva (probabilidad pos-prueba). E(+) & P(+): Enfermedad y prueba positiva, E(+) & P(-): Enfermedad y prueba negativa, E(-) & P(+): No enfermedad y prueba positiva, E(-) & P(-): No enfermedad y prueba negativa.
Probabilidad
Ya que la probabilidad se incrementó, pero quedó ubicada aun en un valor de la escala de probabilidades extremadamente bajo, es muy claro que la mamografía, aun con un resultado positivo no ha ayudado de manera significativa para la toma de una decisión (resecar la lesión vs. tranquilizar y olvidarse del tema) en esta paciente, y este valor se convertirá ahora en la probabilidad pre-prueba de próximos datos.
Si quisiésemos en éste momento apelar a otra prueba diagnóstica, deberíamos utilizar alguna con una sensibilidad muy cercana al 100% (inexistente en el cáncer de seno) con el objeto de que, si sale negativa, descarte, por el momento, esta enfermedad. Desafortunadamente la mayoría de las pruebas diagnósticas en cáncer de mama son más específicas que sensibles1 .
Por otro lado, asumamos por un instante, sólo con fines pedagógicos, que nuestra paciente tiene otros factores de riesgo, que la ubican en una probabilidad pre-prueba inicial del 10%. A cuánto ascendería su probabilidad pos-prueba si tuviese una mamografía positiva?. Intente dar una respuesta siguiendo los pasos anteriores utilizando el mismo rendimiento de la mamografía.
En éste caso la probabilidad ascendió a 47% (espero que haya coincidido) y quedó colocada ahora en un punto adecuado para ser confirmado por una de las tantas pruebas específicas existentes.
Queda entonces claro, que el principal elemento en la función Bayesiana es el valor de la probabilidad pre-prueba, que es cambiante de país a país y de nivel de atención.
Conclusión
Digamos para concluir, que ante condiciones poco prevalentes (con probabilidades pre-prueba muy bajas), que suelen presentarse en niveles primarios de atención ambulatorio o comunitario, se deben seleccionar dentro del arsenal disponible las pruebas diagnósticas con alta sensibilidad esperando un resultado negativo para descartar. En este caso, resultados intermedios ascienden muy poco dicha probabilidad pre-prueba.
Por otro lado, en condiciones muy prevalentes, como las que suelen verse en hospitales de III y IV nivel, deberían utilizarse pruebas altamente específicas con el fin de confirmarlas dado su resultado positivo. La negatividad de pruebas en ese escenario, reduce muy levemente dichas probabilidades pos-prueba.
El problema diagnóstico realmente es de los clínicos, y es formidable cuando quiera que las incertidumbres reinantes acerca de una enfermedad se encuentren aun a mitad de camino de sus umbrales de confirmación o de exclusión. Desafortunadamente éste último escenario es la forma más frecuente de presentación de los pacientes con sus enfermedades o molestias en la práctica clínica cotidiana.
El presente capítulo, pertenece al libro: “La ciencia y el arte del proceso diagnóstico: Una aproximación desde la Medicina Basada en Evidencias”®, de Jairo Echeverry Raad, que será publicado en el 2004. Está siendo cedido sin cargo, para ser utilizado por los lectores de la Revista Colombiana de Neumología. Para uso personal y académico exclusivamente. Cualquiera otra utilización requiere permiso explícito del autor. Todos los derechos reservados.
Bibliografía
1. Mushlin AF. Diagnostic test in breast cancer: Clinical strategies based on diagnostic probabilities. Ann Intern Med 1985:1030-79.
2. Brown ML, Houn F, Sickles EA, Kessler LG. Screening mammography in community practice: positive predictive value of abnormal findings and yield of follow-up diagnostic procedures. AJR Am J Roentgenol 1995; 165:1373-7.
3. Echeverry J, Ardila E. Pruebas Diagnósticas y Proceso Diagnóstico. En: Estrategias de Investigación en medicina Clínica. Ardila E, Sánchez R, Echeverry J. Editores. 1ª Edición 2000. El Manual Moderno. Bogotá; Capítulo 13.
4. Echeverry J. Definiendo Enfermedad. Rev Col Neumol 2003; 15(2):69-81.
5. Sox HC, Blatt MA, Higgins MC, Marton JI. Medical Decision Making. Butterworths Publishers, 1988. Boston USA; Chapter two.
6. Nkanginieme KEO. Clinical Diagnosis as a Dynamic Cognitive Process: Application of Bloom’s Taxonomy for Educational Objectives in the Cognitive Domain. Med Educ Online [serial online] 1997; 2:1. Available from: URL https://www.utmb.edu/meo/
7. Godolphi W. The role of risk communication in shared decision making. BMJ 2003;327:692-3.
8. TM. Abdelhamid. The Multidimensional Learning Model: A Novel Cognitive Psychology-Based Model for Computer Assisted Instruction in Order to Improve Learning in Medical Students. Med Educ Online [serial online] 1999;1,1. Available. URL https://www.Med-Ed-Online.org.
9. Kahneman D, Slovic P, Tversky A. eds. Judgment under uncertainty: heuristic and biases. Cambridge: Cambridge Univ Press, 1982.
10. Tvuersky A, Kahneman D. Judgment under uncertainty: heuristic and biases. Science 1974;185:1124 – 31.
11. Slotnik HB, Mejicano G, Passin SM, Bailey A. The epidemiology of physician learning. Medical Teacher 2002; 24(3):304-12.
12. Miller GA. The magic number seven plus or minus two: some limits on our capacity for processing information. Psychol Rev 1956;63:81-97
13. Sox HC, Blatt MA, Higgins MC, Marton KI. Medical Decision Making. Boston: Butterworth Publishers, Boston USA. Chapter three. 1988.
14. Sox HC, Blatt MA, Higgins MC, Marton JI. Medical Decision Making. Butterworths Publishers, Boston USA. Chapter four. 1988.
15. Hoffrage U, Linsey S, Hertwig R, Gingerenzer G. Commutating statistical information. Science 2000;290:2261-62.
16. Steuer J, Fischer JE, Bachmann LM, Soller M, Riet Gt. Communicating accuracy of test to general practitioners: a controlled study. BMJ 2002;324:824-26.
17. Hirsch R, Riegelman RK. Probability. In: Hirsch R, Riegelman R Eds. Statistical First Aid: Interpretation of Health Research Data. Blackwell Scientific Publications, USA. 1992. Pp 3 –20.
18. B. Fundamentals of Biostatistics. Duxbury Press. California USA. 3ª edition. 1990:51 – 59.
19. Gingerenzer G, Edwards A. Simple tools for understanding risks: from innumeracy to insight. BMJ 2003;327:741-44.
20. https://cebm.jr2.ox.ac.uk/
21. Feuer EJ, Wun LM, DevCan:probability of developing or dying of cancer. 4.1. Bethesda, Md.: National Cancer Institute, 1999.
22. Sox HC. Exercise testing in suspected coronary artery disease. Disease-a- month. December 1985.
23. McGee S. Evidence-based physical diagnosis. W.B. Saunders Company. Philadelphia, PA, USA. 2001
24. Wasson JH, Sox HC, Goldman L, Neff RK. Clinical Prediction Rules: applications and methodologic standards. N Engl J Med 1985; 313:193 – 200.
25. https://bcra.nci.nih.gov/brc/
26. The Women’s Health Initiative. Risks and Benefits of Estrogens Plus Progestin in Healthy Postmenopausal Women: Principal Results From the Women’s Health Initiative Randomized Controlled Trial. JAMA 2002; Vol.288 (3):321-333.
27. Fletcher S, Elmore JG. Mammography screening for breast cancer. N Engl J Med 2003;348:1672-80.
28. Sacket DEL, Haynes RB, Tugwell P. Clinical Epidemiology. A basic science for clinical medicine. Boston: Little, Brrown and Company 1985.
29. Knapp RG, Miller MC. Describing the Performance of a Diagnostic Test In:. Knapp RG, Miller MC. Clinical epidemiology and biostatistics. Malvern (Pennsylvania): Harwal Publishing Company, 1992: 31 –51.
30. Suchman AL, Dolan JG. Odds and Likelihood Ratio. In: Griner, Panzer RJ, Greenland P, eds. Clinical diagnosis and the laboratory . Logical strategies for common medical problems. Chicago: Year Book Medical Publisher, 1986:36 –43.
31. Yerushalmy J. Statistical problems in assessing methods of medical diagnosis with special reference to X-ray techniques. Public Health Reports 1947;62:1432 – 1449.
32. Olsen O, Gotzsche PC. Cochrane review on screening for breast cancer with mammography. Lancet 2001;355:129-34.
33. Brown ML,Houn F,Sickles EA,Kessler LG. Screening mammography in community practice: positive predictive value of abnormal findings and yield of follow-up diagnostic procedures. AJR Am J Roentgenol 1995;165: 1373-7.
34. Elmore JG, Barton MB, Moceri VM, Polk S, Arena PJ, Fletcher SW. Ten-Year Risk Of False Positive Screening Mammograms And Clinical Breast Examinations. N Engl J Med 2003; 338(16): 1089 -96
35. Seldmeier P. Improving statistical reasoning: theoretical models and practical implications. Mahwah NJ,Lawrence Erlbaum. 1999.
36. Gigerenzer G, Hoffrage U. Using natural frequencies to improve diagnostic inferences. Academic Medicine 1998;73:538-40.
37. Fletcher S, Elmore J. Mammography screening for breast cancer. N Engl J Med 2003;348(17):1672-80.