Utilidad de la razón de verosimilitud (likelihood ratio) en la práctica clínica

Rincón Epidemiológico

William Otero R, M.D., Internista, Gastroenterólogo, Universidad Nacional De Colombia; Estudiante De Postgrado De Epidemiología, Colegio Mayor De Nuestra Señora Del Rosario;
Jefe De Gastroenterología, Clínica Fundadores; Docente De Gastroenterología, Universidad Nacional De Colombia.
Luis F. Pineda O, M.D., Internista Gastroenterólogo, Hospital Militar Central, Centro De Enfermedades Digestivas,
Centro Médico Almirante Colón; Gastroenterólogo, Hospital El Tunal;
Estudiante De Postgrado De Epidemiología, Colegio Mayor De Nuestra Señora Del Rosario.
Luis H. Beltrán Ch., M.D., Gineco-Obstetra, Universidad Nacional De Colombia, Coordinador, Departamento De Ginecoobstetricia, Policlínico Del Olaya, Estudiante De Postgrado De Epidemiología,
Colegio Mayor De Nuestra Señora Del Rosario.Bogotá, D.C. Rev Colomb Gastroenterol 2001; 16: 33-36.

La piedra angular para el adecuado tratamiento de las enfermedades es un diagnóstico correcto.

Para lograrlo, los médicos competentes son conscientes de la necesidad de una cuidadosa historia clínica que incluya un buen examen físico.

No obstante el conocimiento de la literatura disponible, la adecuada interpretación de la misma y la habilidad del clínico, usualmente son necesarios algunos exámenes de laboratorio para confirmar un diagnóstico.

Al no poder aplicar, en la mayoría de los casos pruebas diagnósticas perfectas o estándares de oro (gold standard), los exámenes solamente podrán aumentar o disminuir la probabilidad (likelihood )del diagnóstico de una enfermedad (1).

En la práctica diaria, el proceso para llegar a un diagnóstico es imperfecto y debemos ser conscientes de que la presunción diagnóstica es una probabilidad y con frecuencia no se tiene la certidumbre de un diagnóstico definitivo, incluso después de múltiples pruebas utilizadas en serie o en paralelo.

Para la interpretación y la elección de las diferentes pruebas diagnósticas, es necesario estar familiarizado con algunos conceptos básicos, por ejemplo, la razón de verosimilitud (RV) o razón de probabilidades (likelihood ratio), que será el motivo de la presente revisión.

Tradicionalmente, la exactitud de una prueba diagnóstica para detectar o excluir una enfermedad se expresa en términos de sensibilidad, especificidad, valor predictivo positivo y valor predictivo negativo (2), todas las cuales son proporciones o probabilidades que se organizan de manera muy sencilla en una tabla de 2 x 2 o tablas de contingencia (Figura 1).

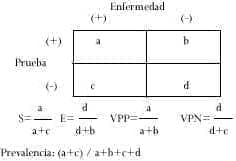
Figura 1.Tabla de 2 x 2.

Sensibilidad (S):

Es la proporción o porcentaje de individuos con la enfermedad,que tienen un resultado positivo de una prueba determinada; en la Figura 1, se representa por a/ (a+c) = verdaderos positivos / (verdaderos positivos + falsos negativos).

Como nemotecnia, se puede usar la palabra PID (positive in disease ) (1): una prueba muy sensible rara vez no detecta la enfermedad (1-5).

Otra palabra nemotécnica es SENEX: si una prueba es muy SEensible, un resultado Negativo Excluye la enfermedad (6).

Especificidad (E):

Es complementario de la sensibilidad y representa la proporción o el porcentaje de individuos sin la enfermedad que tienen negativo el resultado de una prueba; en la Figura 1 se representa por d/(b+d) = verdaderos negativos / (falsos positivos + verdaderos negativos).

La palabra nemotécnica es NIH (negative in health) (1): una prueba muy específica rara vez es positiva en individuos sin la enfermedad y, por tanto, no clasifica como enfermos a las personas sanas. Por lo anterior, la utilidad de una prueba específica es mayor cuando su resultado es positivo (1,2).

Otra palabra nemotécnica es ESPIN: cuando una prueba es muy Específica, un resultado Positivo Incluye la enfermedad (6).

Pruebas muy sensibles serán útiles en los programas de tamizaje (screening), en los cuales se intenta detectar enfermos entre personas aparentemente sanas, o en las evaluaciones iniciales de los pacientes, cuando existen varias posibilidades diagnósticas, para descartar algunas de ellas.

Para el diagnóstico definitivo:

Se necesita una prueba muy específica, es decir, aquella que no sea positiva en los sanos; en otras palabras, la especificidad es útil para confirmar un diagnóstico, sugerido por pruebas muy sensibles, ya que éstas pueden dar resultados falsos positivos (1-3).

La sensibilidad y la especificidad se determinan en poblaciones específicas, enfermas o sanas (1, 4), y, por tanto, en un paciente individual de la consulta diaria, del que no se sabe si está sano o enfermo, los valores de sensibilidad y especificidad no permiten determinar si el individuo tiene la enfermedad que se le investiga.

Si una prueba con una sensibilidad y especificidad del 95% fuera positiva en un paciente y éste le preguntara al médico si tiene o no la enfermedad, lo máximo que éste podría decirle es que, de 100 pacientes que tienen la enfermedad, la prueba es positiva en 95 y entre 100 pacientes sin la enfermedad, ésta es negativa en 95; es decir, la sensibilidad por sí misma no hace el diagnóstico como tampoco la especificidad por sí misma lo descarta.

Es difícil interpretar los resultados de un examen en un paciente conociendo solamente su sensibilidad y especificidad (4). En el caso hipotético que mencionamos, la información que recibe el paciente no le aclara la probabilidad de tener o no la enfermedad.

Para dar una mejor información, es necesario conocer los valores predictivos, tanto positivo como negativo, de la prueba: las probabilidades de que un resultado positivo o negativo sea o no un falso positivo o un falso negativo respectivamente.

 

Valor predictivo positivo de una prueba (VPP):

Es la probabilidad (o proporción) de tener realmente la enfermedad, cuando su resultado es positivo. En la Figura 1 corresponde a: a/(a+b)=verdaderos positivos/(verdaderos positivos+falsos positivos) (1-3).

Valor predictivo negativo de una prueba (VPN):

Es la probabilidad (o proporción) de no tener la enfermedad cuando el resultado es negativo. En la Figura 1, corresponde a: d / (d+c) = (verdaderos negativos) / (falsos negativos + verdaderos negativos) (1-3).

Los valores predictivos de una prueba determinada no son una característica o una propiedad intrínseca de la prueba, ya que dependen de la sensibilidad, la especificidad y la prevalencia de la enfermedad en la población que está siendo evaluada (qué tan común es la enfermedad en la población a la que pertenece el paciente) (1-5), como se ve en la Tabla 1.

Los valores predictivos, también se conocen como probabilidades post-prueba y, la prevalencia de la enfermedad, como probabilidad pre-prueba (1, 2, 4).

Esta última refleja la probabilidad de que un paciente tenga la enfermedad sin haberle realizado una prueba diagnóstica. Concretamente la prevalencia se aplica a las poblaciones y la probabilidad pre-prueba se aplica a los individuos (4).

Tabla 1. Variaciones en el VPP y el VPN, con la
prevalencia de la enfermedad; S y E de 90%.

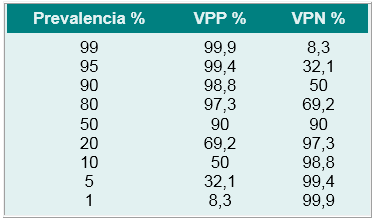
Modificado de Ref. 5

A mayor sensibilidad de una prueba, mejor es su VPN; es decir; hay más seguridad de que no exista la enfermedad, cuando el resultado es negativo, (1, 2) y, cuanto más específica, mejor es su VPP; hay más seguridad de la existencia de la enfermedad, cuando una prueba es positiva (1, 2).

Sin embargo, como el resultado final es influido por la prevalencia, los resultados positivos de una prueba altamente específica en un alto porcentaje pueden ser falsos positivos, en pacientes con baja probabilidad de tener una enfermedad (1, 2, 7).

En los datos de la Tabla 1, se puede ver cómo los valores predictivos se modifican con la prevalencia de la enfermedad.

Cuando una prueba con S y E del 90% es positiva y se analiza con una prevalencia del 20%, el VPP es de 69,2% y el VPN es de 97,3%; estos valores son diferentes cuando la prevalencia es del 90%, ya que serían 98,8 prueba también se acerca a cero; al contrario, si la prevalencia de la enfermedad se acerca a 100%, los resultados negativos de una prueba altamente sensible son falsos negativos y, por tanto, su valor predictivo negativo es muy bajo, cercano a cero (1, 2, 7).

Un ejemplo de la interacción de estas probabilidades:

Es lo que ocurre con el diagnóstico de la hepatitis por virus C. La prueba inmunoenzimática (IEE-3) es la primera prueba de tamizaje que se realiza para el diagnóstico de la hepatitis C (sensibilidad, 97%), pero, en donadores de sangre en áreas de baja prevalencia, el RIBA (recombinant immunoblot assay ) (que es más específico) sigue siendo útil para determinar si un IEE positivo es un verdadero o un falso positivo (8, 9).

En poblaciones con baja prevalencia de hepatitis C, el anti-C es falso positivo en 40% de los casos (10).

Lo mismo ocurre en individuos con anti-C positivo, sin factores de riesgo para hepatitis C y ALT normal. En áreas de alta prevalencia y para pacientes con riesgo de padecer hepatitis C, el resultado del anti-C tiene un alto valor predictivo positivo y por, tanto, es suficiente para el diagnóstico y hace innecesario el RIBA (8, 9, 11).

Asimismo en pacientes con anti-C positivo en un programa de donación de sangre, el ARN positivo confirma el diagnóstico, pero, un ARN negativo indica un resultado falso positivo del anti-C o una infección con el virus C resuelta (8).

La incertidumbre se resuelve con un RIBA: si es negativo, indica que el anti-C era falso positivo y, si es positivo, indica infección por virus C resuelta (8).

Valores predictivos se modifican con la prevalencia de la enfermedad

Como los valores predictivos se modifican con la prevalencia de la enfermedad y los valores que ocasionalmente incluyen los fabricantes de las pruebas provienen de estudios hechos en pacientes de hospitales de referencia, no se puede asumir que el rendimiento de la prueba sea igual en otras poblaciones (1, 4).

RV no es influida por la prevalencia de la enfermedad y, por tanto, es la medida de exactitud que se prefiere en la actualidad cuando se interpretan los resultados de un paciente individual (1, 2, 4).

La RV proviene del teorema matemático de Bayes, el cual establece que: odds pre-prueba x/RV = odds post-prueba (1, 2, 4, 5). La RV se puede calcular conociendo la sensibilidad y la especificidad como se mencionará más adelante.

Matemáticamente, RV = odds post-prueba/odds pre-prueba. Indudablemente, esta terminología es algo confusa para los médicos que estamos acostumbrados a referirnos en términos de probabilidades y no de odds.

La probabilidad, como hemos mencionado, se utiliza para expresar la sensibilidad, la especificidad, el VPP y el VPN, y significa el porcentaje de una población en la cual se presenta una característica (por ejemplo, una prueba de laboratorio positiva).

La odds ratio se refiere a la probabilidad de que un fenómeno ocurra dividido por la probabilidad de que no ocurra y es un término usual en el argot de las apuestas de las carreras de caballos o en los partidos de fútbol.

La odds ratio de que un caballo gane es 1: 4 significa que, por cada probabilidad de que gane, hay 4 probabilidades de que no gane, o que tiene una probabilidad de ganar de 1/5 = 0,2 o de 20% (una probabilidad entre cinco probabilidades).

Matemáticamente,

De esta fórmula se puede despejar:

Matemáticamente, la RV es la relación de dos pro babilidades. Es un método alternativo para evaluar el rendimiento de una prueba diagnóstica con resultados dicotómicos (positivo o negativo) y no dicotómicos (1-5).

Para el primer caso, hay pruebas con RV positiva y RV negativa.

RV = probabilidad de un resultado particular en pacientes con la enfermedad, dividida por la probabilidad del mismo resultado en pacientes sin la enfermedad (1-5).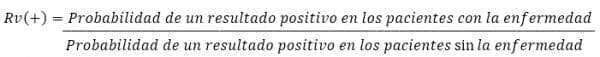

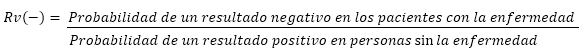
Entre más alta sea la RV:

Para una prueba positiva, mejor es la prueba para diagnosticar la enfermedad y, entre más baja la RV para una prueba negativa, mejor es la prueba para excluir la enfermedad (4). Como regla general, son útiles clínicamente las pruebas con RV (+) mayor de 10 y con RV (-) menor de 0,1 (4).

Sencillamente, una RV mayor de 10 significa que la odds ratio de la enfermedad es 10 veces mayor después de la prueba o, dicho en otras palabras, por cada 10 veces que la prueba sea positiva en los pacientes con la enfermedad (numerador), es positiva en un paciente sin la enfermedad (denominador).

Una RV negativa menor de 0, 1 significa que la odds ratio post-prueba es un décimo de la odds ratio pre-prueba (4), o,q ue la prueba es negativa en 0,1 pacientes con la enfermedad por cada paciente sin la enfermedad.

La RV indica qué tanto una prueba de diagnóstico aumenta o disminuye la probabilidad pre-prueba del desorden que se investiga.

Una RV de 1 significa que la probabilidad post-prueba es exactamente la misma que la probabilidad pre-prueba (13). Las RV(s) mayores de 1 aumentan la probabilidad de que la enfermedad blanco esté presente y, a mayor valor, mayor probabilidad.

Inversamente, los RV(s) menores de 1 disminuyen la probabilidad de la enfermedad blanco y, entre más pequeña, menor probabilidad (13). En la práctica diaria.

Para la interpretación de las RV(s) se pueden tener en cuenta las siguientes consideraciones (13):

a. RV (+) >10 o RV (-) <0, 1, generan grandes cambios, usualmente conclusivos, de la probabilidad pre-prueba.

b. RV (s) +de 5 a 10 y RV (-) de 0,1 a 0,2, generan moderados cambios en la probabilidad preprueba.

c. RV (+) de 2 a 5 y RV (-), generan pequeños cambios en la probabilidad.

d. RV (+) de 1 a 2 y RV (-) de 0, 5 a 1, alteran la probabilidad en un grado pequeño (rara vez importante).

Para hacer el cálculo de la probabilidad postprueba, se debe transformar la probabilidad preprueba a odds pre-prueba y, después, ésta se multiplica por la RV para generar una odds post-prueba, la cual finalmente se transforma en una probabilidad postprueba.

Este paso matemático se puede obviar utilizando un nomograma en el cual, conociendo la probabilidad pre-prueba y la RV, se calcula la probabilidad post-prueba trazando una línea que intercepte la RV (7).

Las razones de verosimilitud de los exámenes que pueden dar múltiples resultados continuos:

Se evalúan representándolas en una curva ROC (receiver operating characteristic curve ), que relaciona la tasa de verdaderos positivos (sensibilidad) en la ordenada con la tasa de falsos positivos (1-especificidad) en la abscisa (2, 4).

Las curvas ROC son útiles para relacionar el equilibrio entre la sensibilidad y la especificidad de una prueba y se pueden utilizar para ayudar a decidir dónde debe estar el mejor punto de corte (1, 12). La descripción de esta importante herramienta está fuera del alcance de esta publicación.

La denominación ROC de estas curvas proviene de la teoría de detección de la señal, desarrollada durante la segunda guerra mundial para el análisis de las imágenes del radar (12).

Los operadores del radar tenían que decidir si un bache de radar sobre la pantalla representaba una señal amiga o enemiga, o simplemente un artefacto. La teoría de la detección de la señal mide la capacidad de los receptores de radar para hacer tales discriminaciones.

La capacidad para hacerlo fue denominada receiver operating characteristic (ROC) y, desde 1970, esa teoría de detección de la señal fue reconocida como una herramienta útil para interpretar los resultados de los exámenes utilizados en medicina (12).

Conclusiones

1. La RV es un método clínicamente útil para expresar la exactitud de una prueba y no es influido por la prevalencia de las enfermedades.
2. La RV es fácil de calcular, si se conocen la sensibilidad y la especificidad de una prueba.
3. La magnitud de la RV indica la capacidad de una determinada prueba para hacer o para excluir un diagnóstico.
4. La costumbre de los clínicos de interpretar los resultados de una prueba en términos de probabilidades y no de odds, explica en parte que la RV no se utilice tan frecuentemente en la literatura médica (por ahora).
5. La RV sir ve para las pruebas con resultados dicotómicos o múltiples (RV multinivel).
6. Computa las odds post-pruebas después de una serie de pruebas diagnósticas, es mucho más fácil que utilizar el método sensibilidad / especificidad.

Odds post-prueba = odds pre-prueba X RV1, X RV2, x ……. RVn. 7. La RV (+) clínicamente útil debe ser mayor de 10 y, la RV (-), menor de 0, 1.

Referencias

• 1. Go AS. Refining probability: an introduction to the use o diagnostic tests. In: Friedland DJ, editor. A Lange medical book evidence-based medicine, Stanford, Connecticut: Appleton & Lange; 1998 p.11-33.
• 2. Fletcher RH, Fletcher SW, Wagner EH. Epidemiología clínica.2a edición. Madrid, España: Masson, Williams & Wilkins; 1998.
• 3. Sheps SB,S chechter MT. The assessment of diagnostic tests. A survey of current medical research. JAMA 1984; 252: 2418-22.
• 4. Mant J. Is the test effective? In: Dawes M, Davies P, Gray A, et al, editors. Evidence-based practice. Toronto:C hurchill Livingstone; 1999 p.133-137.
• 5. Moayyedi P, Axon ATR. The usefulness of the likelihood ratio in the diagnosis of dyspepsia and gastroesophageal reflux disease Am J Gastroenterol 1999; 94: 3122-5.
• 6. Sackett D, Haynes B, Guyatt G, et al. Epidemiología clínica: ciencia básica para la medicina clínica. Segunda edición; Madrid: Editorial Panamericana; 1994.
• 7. Fagan TJ. Nomogram for Baye ´s Theorem. N Engl J Med 1975; 293: 257.
• 8. Morishima C, Gretch DR. Clinical use of hepatitis C virus tests for diagnosis and monitoring during therapy. Clin Liver Dis 1999; 3: 717-40.
• 9. Schiff E, De Medina M, Kahn RS. New perspectives in the diagnosis of hepatitis C. Sem Liver Dis 1999; 19: S3-S15.
• 10. Atrah HI, Hutchinson F, Gough D, et al. Hepatitis C virus seroconversión rate in established blood donors. J Med Virol 1995; 46: 329-33.
• 11. Paulotsky JM, Germanidis G, Neumann AU, et al. What strategy should be used for diagnosis of hepatitis C virus infection in clinical laboratories ? Hepatology 1998; 27: 177-82.
• 12. https://im.unmc.edu/dxtests/roc3.htm
• 13. Jaeschke R, Guyatt GH, Sackett DL. How to use an article about a diagnostic test. https://www.cche.net/principles/content_diagnosis.asp y 50%, respectivamente. A medida que la prevalencia de la enfermedad se acerca a cero, el valor predictivo positivo