El Encuentro entre la Medicina y la Matemática

Resumen

El encuentro entre la medicina y las matemáticas va mucho más allá de la modelación estadística o la biofísica.

La matemática aplicada en medicina es la fuente principal de los modelos avanzados de analítica, pero a la vez permite optimizar la minería de datos, los métodos de visualización, la algoritmización y posteriormente los razonadores alojados en plataformas de salud.

Presentamos en este capítulo un breve resumen de las técnicas matemáticas de mayor uso para la evolución de la medicina computacional y su posterior migración a modelos mecanicistas.

Palabras clave: Matemáticas; Medicina; Minería de Datos; Modelos de Optimización; Redes Bayesianas; Redes Neuronales; K-means; Análisis Multicriterio; Ecosistemas Digitales en Salud; Reasoner.

The Encounter between Medicine and Mathematics

Abstract

The encounter between medicine and mathematics goes far beyond statistical modeling or biophysics. Applied mathematics in medicine is the main source of advanced analytical models, but at the same time it allows optimizing data mining, visualization methods, algorithms and later what is known as reasoners hosted on health platforms.

We present in this chapter a summary of the most widely used mathematical techniques for the evolution of computational medicine and its subsequent migration to mechanistic models.

Keywords: Mathematics; Medicine; Data Mining; Optimization Models; Bayesian Networks; Neural Networks; K-means; Multicriteria Analysis; Digital Ecosystems in Health; Reasoner.

Introducción – Encuentro entre la Medicina y la Matemática

El encuentro entre la medicina moderna y las matemáticas es un acontecimiento borroso en la bruma del tiempo. Daniele Bernoulli en 1760 utilizando la tabla de vida de Halley y algunos datos sobre la viruela, demostró que la vacunación era ventajosa si el riesgo asociado de muerte era inferior al 11% ⁽¹⁾.

Fue este el primer modelo matemático en la historia de la epidemiología.

Aparentemente, el hecho de que las matemáticas puedan contribuir a la biología y la medicina no se conoce suficiente. Ciertamente, todo el mundo sabe que la estadística es una herramienta esencial para validar los resultados de la investigación en biología y medicina, pero la mayoría de las veces no creemos que pueda ir más allá.

Las matemáticas tienen mucho que decir sobre la comprensión de los seres vivos y sobre cómo se conserva mejor la vida en nuestra civilización.

Abundan los ejemplos, entre ellos el estudio del genoma, la estructura espacial de moléculas vivas (ADN, ARN, proteínas):

El estudio de los ecosistemas genéticos de las poblaciones, la filogenética, la epidemiología, la teoría de la evolución, etc.

Cabe señalar que no se trata de una aplicación de la matemática (en el sentido de que ya se conocerían las teorías matemáticas involucradas, y que simplemente sería cuestión de utilizarlas), sino de matemática aplicada, porque la interacción entre la medicina y la matemática es una relación compleja con múltiples variables y una dinámica bidireccional que requiere creatividad y capacidad de tender puentes entre las ciencias, un movimiento transdisciplinario.

El modelo de Daniel Bernoulli recibió una percepción mixta en ese momento (fue notable y erróneamente criticado por d’Alembert), pero se considera hoy como el texto fundacional de la epidemiología moderna, lo que lo convierte en un pionero del modelado matemático en medicina, que hoy se refiere a materias verdaderamente diversas (matemáticas y deportes, por ejemplo), pero es en la investigación del cáncer en el que hemos demostrado que las matemáticas aplicadas tienen mucho más que decir, y aún más con la creciente complejidad de la medicina genómica o de precisión.

La investigación del cáncer se refiere al uso de modelos matemáticos para integrar la complejidad biológica y proporcionar herramientas algorítmicas que optimicen la evaluación de la eficacia de los tratamientos contra el cáncer:

Al tiempo que se limitan sus efectos tóxicos. La pregunta es bastante simple: para que un medicamento contra el cáncer sea eficaz, el ingrediente activo debe estar presente en la sangre del paciente en cantidad suficiente (intensidad de la dosis), pero muy a menudo estos medicamentos son muy tóxicos por encima de una dosis específica.

Por lo tanto, la concentración del fármaco debe mantenerse constantemente entre estos dos niveles: el suficiente para que cause un efecto curativo, pero no demasiado para crear efectos secundarios.

Podemos, a partir de un análisis detallado e individualizado, determinar la reacción de cada paciente a la medicación con el apoyo de farmacogenómica (donde este aplique) y modelos predictivos. Esos modelos podrían asignarse a ecosistemas digitales que permitan una farmacovigilancia inteligente.

Si la pregunta es simple, la respuesta es compleja: debemos utilizar matemáticas avanzadas como ecuaciones diferenciales, derivadas parciales o teoría del control para determinar las estrategias óptimas para administrar la medicación.

Pero con las matemáticas, también podemos intentar mejorar el sistema general a cargo de brindar una mejor atención médica. El arsenal matemático se liberó con la computación y la era digital. Los inicios de la computadora están íntimamente ligados a las matemáticas. Las primeras máquinas se construyeron para realizar cálculos balísticos o contables.

Cuando la informática se convirtió en una disciplina por derecho propio, en los años 1960-1980, también fue sobre el modelo de la historia de las matemáticas que a su vez comenzó a escribir la propia.

Desde la década de 1960, la historiografía de la informática se ha ido diversificando y enriqueciendo gradualmente en relación con la progresiva diversificación del uso de la computadora.

Pero hay que destacar que esta historiografía buscó primero un modelo y legitimidad en la historia de las matemáticas.

Si la historia de la informática ha heredado innegablemente la historia de las matemáticas, hoy también podemos plantearnos la pregunta contraria: ¿puede la historia de la informática inspirar la historia de las matemáticas? El nacimiento de la computadora sin duda ha renovado el interés de los historiadores por ciertos aspectos de las matemáticas, como las cuestiones de aproximación y precisión en el cálculo numérico, las apuestas de los recursos de tiempo y memoria necesarios para ejecutar un algoritmo, la organización lógica de complejos programas, etc.

Todos estos aspectos no solo ayudaron a organizar la computación en una computadora, sino que también estimularon el desarrollo de nuevas ramas de las matemáticas y la lógica.

Esta capacidad precisa de resolución práctica de problemas, derivada de la evolución de las tecnologías de la información dio origen a la medicina computacional y un nuevo paradigma en las ciencias médicas a la que llamaremos Medicina de Última Generación o NGM por sus siglas en inglés Next-Gen Medicine.

NGM utilizará una gama completa de herramientas de inspiración matemática, como análisis y aprendizaje automatizado (AA), en un escenario donde la complejidad incremental se debe al tipo de solución requerida.

Para poder abordar este nuevo paradigma iniciaremos con el abordaje de los datos, lo que denominamos la pirámide de la complejidad matemática; posteriormente entraremos en los análisis de la hipercomplejidad y finalizaremos con el concepto de razonador y ecosistemas digitales en medicina.

La pirámide de la complejidad matemática

Analítica matemática descriptiva

Este nivel corresponde al de consulta inicial, al ¿qué ocurre? ¿cuántos?, ¿en dónde?, ¿qué tan frecuente? La solución técnica es la presentación de informes. La mayor parte de la industria de la salud está vinculada a este campo de bajo nivel que es completamente lineal.

El segundo nivel de análisis descriptivo es una consulta, que es la solución técnica para responder a la pregunta de cuál es el problema. Esto se basa en matemática frecuentista. Analítica matemática predictiva En el siguiente grado de complejidad matemática, es posible encontrar enfoques técnicos como sistemas de alerta, simulación, pronóstico y modelado predictivo.

Estas soluciones responderán a ¿qué acciones se necesitan, qué podría suceder, qué pasa si estas tendencias continúan y qué sucede a continuación, respectivamente. ¿Qué pasa si, por ejemplo, un factor de riesgo de cáncer específico se elimina de un escenario?

Analítica matemática prescriptiva

Finalmente, el nivel más alto de complejidad matemática consiste en los algoritmos de optimización y algoritmos de optimización estocástica. La optimización responde a cómo lograr el mejor resultado y la optimización estocástica se suma al mejor escenario de resultados, los efectos de la variabilidad. (Figura 1).

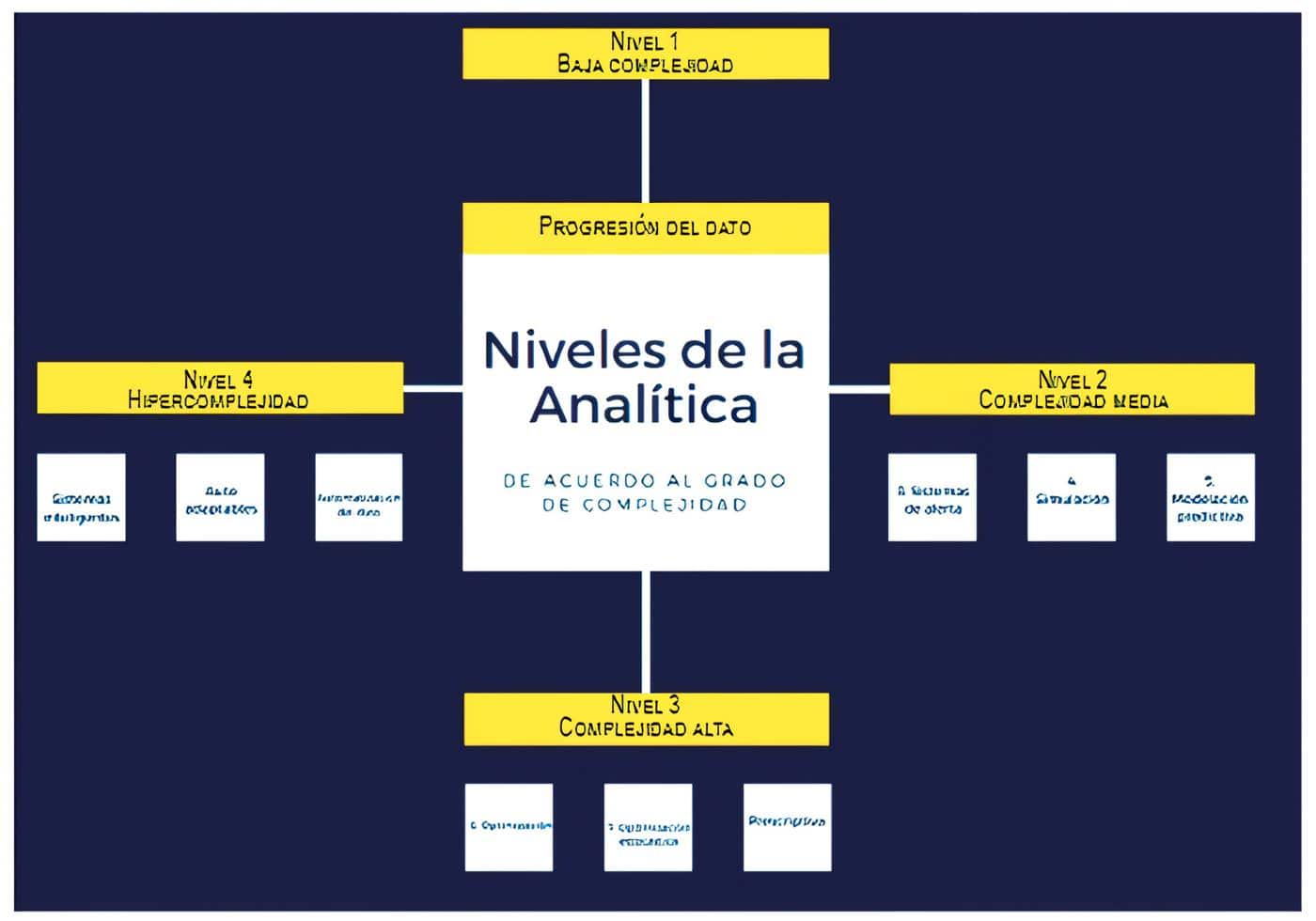
Figura 1. Niveles de complejidad de la analítica matemática (elaboración propia)

Las decisiones clínicas tienen riesgos de sesgo cognitivo como el del anclaje, la disponibilidad heurística, el efecto marco, el de confirmación etc., los cuales repercuten en los resultados finales y, obviamente, crean ineficiencias en la atención médica.

Estos modelos en el escenario de cáncer común, en los que tenemos diferentes tratamientos con desempeño clínico y de seguridad similar, permiten tomar mejores decisiones. El cáncer de pulmón y riñón o el melanoma son hitos de estos marcos. 

Un modelo de optimización aplicado a la medicina tiene que definir los valores positivos a ganar, pero también las restricciones (demográficas, supervivencia, supervivencia libre de progresión, eficacia, dimensión económica de efectos adversos entre otras).

Los modelos de optimización aplicados a la medicina se utilizan para mejorar el diseño o el proceso de prototipado de sistemas complejos ⁽²⁾, que requieren el uso de simuladores o pruebas reales para medir su desempeño.

Estos simuladores pueden ser de diferente naturaleza: simulaciones digitales de fenómenos físicos (por ejemplo, del tipo de elemento finito) o simulaciones de eventos. A menudo requieren importantes recursos informáticos.

Por tanto, es importante aplicar una estrategia de investigación económica en cuanto al número de evaluaciones. Por este motivo lo que se recomienda es el uso de diferentes metodologías de minería y análisis de los datos para tratar el problema de salud específico.

Pero supongamos que el concepto está ahora en el corazón del proceso, el cual manipula grandes volúmenes de datos sin procesar para encontrar conocimiento útil.

En ese caso, se trata de la extracción de conocimientos relevantes que conduzcan a la toma de decisiones. Los métodos estadísticos analizan principalmente datos “históricos” elementales de la gestión actual.

La minería de datos se centra en los datos que circulan en los sistemas de información de las entidades administrativas, empresas u organizaciones y, a través de ellas, del entorno hospitalario o médico.

Métodos de minería de datos

Los métodos de minería de datos son diversos y los que se elijan deben basarse en varias consideraciones, tales como:

• La tarea para resolver,
• La naturaleza y disponibilidad de los datos y
• El propósito del modelo construido.

Sin embargo, los métodos que se presentan a continuación siguen siendo los más importantes. Cabe destacar que no existe un método mejor ya que cada uno tiene sus ventajas y desventajas. A modo de resumen son ⁽²⁾:

Métodos de visualización

Permiten realizar análisis exploratorios para identificar patrones, estructuras, síntesis, etc. Estos como su nombre lo indica están basados en gráficos que facilitan la interpretación de los resultados.

Los métodos más utilizados son gráficos de estadísticas elementales (media, desviación estándar, varianza), histogramas, nubes de puntos y curvas. Este método es el que usualmente observamos en los tableros de inteligencia de negocios institucionales (BI).

Árboles de decisión

Estas son estructuras que representan conjuntos de decisiones. Estas decisiones generan reglas para la clasificación de la recolección de datos, por lo que es una representación gráfica de un procedimiento de clasificación, que predice variables discretas ⁽³⁾.

Los nodos internos del árbol son pruebas sobre los atributos y las hojas son las clases. Por lo tanto, un árbol de decisiones puede verse como un conjunto de reglas que conducen a una clase.

Se establece una correspondencia entre un objeto descrito por un conjunto de características (atributos) y un conjunto de clases disjuntas.

La hoja de cada árbol denota una clase y cada nodo interno una prueba para uno o más atributos, produciendo un subárbol de decisión para cada posible resultado de la prueba. Un algoritmo apropiado puede basarse en este tipo de estructura que algunos llaman de “IF/THEN”.

Redes neuronales

Estos son modelos predictivos que utilizan datos existentes con un resultado conocido para formar un modelo utilizado en la predicción con resultados desconocidos. Una red neuronal consta de grupos de nodos (neuronas) en los que cada grupo de nodos corresponde a una capa. Está formado por al menos tres capas: entrada, media (u oculta) y salida.

En la capa de entrada, cada nodo corresponde a una variable predictora. Los valores internos de los otros nodos (de las capas intermedias y la capa de salida) se calculan mediante una función de suma. La capa de salida contiene uno o más nodos y las variables para predecir.

La red puede tener varias capas intermedias (pero solo una entrada y una salida), también llamadas capas ocultas. Cada nodo de la capa j está conectado a todos los nodos de la capa j + 1.

A cada arco, se le asocia un peso (un valor) Wij; este es el peso del arco entre el nodo i y el nodo j.

Las redes neuronales son herramientas ampliamente utilizadas para clasificación, estimación, predicción y agrupación. Ellas permiten construir un modelo que predice el valor de una variable a partir de otras variables conocidas llamadas variables predictoras.

Si la variable a predecir es discreta (cualitativa), entonces es una clasificación; si es continua (cuantitativa), es una regresión. Los métodos más utilizados son los de redes multicapa Perceptron y Kohonen ⁽⁴⁾.

No estamos hablando en este contexto de la arquitectura de redes neuronales profundas como las recurrentes (RNN) o las de convolución (CNN) que son más complejas y que se utilizan especialmente en los desarrollos de procesadores de lenguaje natural o en visión de máquina.

Redes Bayesianas

Estos son modelos gráficos probabilísticos. Son un tipo de gráfico acíclico dirigido, en el que cada nodo representa una variable continua o discreta, y los arcos representan una dependencia probabilística entre un nodo y sus padres.

Si un arco conecta un nodo Y a un nodo Z, entonces Y es el padre de Z y Z es el descendiente de Y. Cada variable es independiente de las variables con las que no está relacionada. Las variables pueden ser continuas o discretas. El valor de la dependencia de la probabilidad pondera cada vínculo entre dos variables ⁽⁵⁾.

Por lo tanto, el valor del arco que conecta Y con Z es P (Z/Y). Las redes bayesianas requieren muchos parámetros para estimar, mientras que, en la mayoría de los casos, la cantidad de datos disponibles es baja. Estas redes fueron utilizadas para la creación de los primeros sistemas inteligentes en medicina a mediados de los años 80’s.

Las máquinas de soporte vectorial (SVM)

Estas pertenecen a una clase de algoritmos de aprendizaje inicialmente definidos por discriminación, es decir, la predicción de una variable cualitativa inicialmente binaria.

Luego generalizaron a la predicción de una variable cuantitativa. Las SVM se pueden utilizar para resolver problemas de discriminación (es decir, para decidir a qué clase pertenece una muestra) o regresión (es decir, para predecir el valor numérico de una variable).

Método K-ppv (K cercanos)

Este es un método dedicado a una clasificación que puede extenderse a tareas de estimación. El método k-ppv es un método de razonamiento basado en casos. Se parte de la idea de tomar decisiones investigando uno o más casos similares ya resueltos en la memoria y se decide a qué clase pertenece un nuevo caso, examinando los k casos similares a él.

Ningún paso de entrenamiento consiste en crear un modelo a partir de una muestra de entrenamiento. Es la muestra de entrenamiento la que conduce al modelo. Está asociado con una función de distancia y una función de elección de clase basada en las clases de los vecinos más cercanos.

El método de K-promedio (k-mean)

El método consiste en dividir los datos en k grupos, k dados por el usuario. Este método comienza con una agrupación aleatoria de datos (en k grupos), luego cada objeto se asigna al grupo más cercano.

Después de realizar la primera iteración, se calculan los promedios de los grupos y el proceso se repite hasta que los grupos se estabilizan. Un ejemplo local de este método es el geovisor de Covid-19 ejecutado por el IETS ⁽⁶⁾.

Inducción de reglas

Es una técnica que permite la identificación de perfiles, asociaciones o estructuras entre ítems u objetos frecuentes en bases de datos. Es decir, se trata de identificar los elementos que suelen aparecer juntos durante un evento.

Esta regla de asociación es una regla de la forma: “Si X e Y entonces Z”, una regla cuya semántica puede establecerse: “Si X e Y aparecen simultáneamente, entonces Z aparece”. Para considerar y expresar esta asociación en forma de regla, es necesario definir cantidades numéricas que se utilizarán para validar su interés, de ahí: apoyo y confianza.

El soporte es la frecuencia de aparición simultánea de los elementos que aparecen en la premisa y la conclusión, a saber: soporte = frecuencia (premisa y conclusión) y confianza = frecuencia (premisa y conclusión) / frecuencia (premisa).

Por lo tanto, se privilegian las reglas cuyo apoyo y confianza son suficientemente altos. Los algoritmos más utilizados en este método son Apriori y FP-Growth.

Modelos ocultos de Markov

Los modelos ocultos de Markov de orden 1 o 2 (HMM1 y HMM2) se utilizan para clasificar diferentes datos temporales o espaciales.

A diferencia de los algoritmos clásicos que dan una respuesta exacta, estos permiten el aprendizaje automático y se utilizan, por ejemplo, en muchos algoritmos de análisis de secuencias biológicas, ya sea para la detección de genes o la detección de patrones excepcionales.

Regresión lineal (método estadístico)

Es una técnica diseñada para predecir el valor de una variable continua. Su objetivo es definir el mejor modelo que asocie una variable cuantitativa “Salida” con varias variables predictoras “Entrada”. A esto se le llama ajustar el modelo a los datos.

Los modelos lineales son los más utilizados. A esto se le llama regresión lineal. La relación que relaciona una variable que se va a predecir Y con otras variables predictoras (Xi) es una ecuación de regresión a menudo en esta forma:

Y = a₀ + a₁ X₁ + a₂ X₂ + … + aₚ Xₚ

Los métodos más utilizados son la regresión simple y la regresión múltiple. Otro tipo de regresión es la logística, técnica estadística que calcula la probabilidad de un evento a partir de un conjunto de variables predictoras. Pero la regresión logística no siempre converge hacia una solución óptima.

Algoritmos genéticos

Se trata de técnicas de optimización metaheurísticas basadas en los principios de la evolución biológica. No son un método completo de minería de datos y no apuntan directamente a ninguna tarea. Vienen a ayudar en el proceso de minería de datos.

Estas heurísticas guían la búsqueda de buenos modelos en un espacio de búsqueda muy grande. Los algoritmos genéticos se basan en principios de selección, cruzamiento y mutación, que son conceptos derivados de la genética.

La principal desventaja de los algoritmos genéticos es el tiempo de ejecución, que es bastante largo. No hay garantía de que la solución óptima al problema en cuestión se obtenga en un tiempo finito, y su complejidad aumenta con el número de reglas utilizadas.

Descubrimiento de conocimientos a partir de datos (KDD)

Con la digitalización de datos de diferentes departamentos hospitalarios, los médicos necesitan combinar datos de todas estas áreas para deducir nueva información que les permita diagnosticar casos que presentan ciertas complejidades ⁽⁸⁾; este cruce de datos se llama: Extracción de conocimientos a partir de datos (KED) o Descubrimiento de conocimientos a partir de datos (KDD).

Este concepto de KDD se remonta a 1989, pero las primeras conferencias sobre el tema se presentaron en 1995. Este concepto surgió con la explosión de la información almacenada tras importantes avances en los métodos de procesamiento y medios de almacenamiento.

Por lo tanto, KDD tiene como objetivo descubrir información valiosa entre grandes cantidades de datos que pueden ayudar a comprender los datos o predecir el comportamiento futuro de esos datos.

La minería de datos, que es la operación clave del proceso KDD, ha utilizado desde entonces varias herramientas estadísticas y de inteligencia artificial para lograr sus objetivos.

Está en la intersección de muchas disciplinas, como el aprendizaje automático, las tecnologías de bases de datos, la estadística, la representación del conocimiento, la inteligencia artificial, los sistemas expertos, etc.

Su extensión a otras disciplinas, encontramos el KDD médico, que se basa en la noción de cruce de datos médicos para ayudar al profesional de la salud a comprender y cuidar a un paciente –como encontrar y explicar las causas y el efecto de un fármaco para promover un tratamiento específico o validar la eficacia de un fármaco–.

En un proceso KDD, hay diferentes partes interesadas, incluido el usuario, el experto en minería de datos, el analista de datos y el analista del dominio de la aplicación, sus perfiles son:

• El usuario es la persona a la que está destinado el sistema KDD. En la mayoría de los casos, el usuario aparece como un experto en la materia y tiene ciertas nociones sobre la minería de datos que le permiten interactuar en las diferentes etapas del proceso,
• El experto en minería de datos es la persona que configura el proceso KDD. A menudo es asistido por el usuario y el analista de datos,
• El analista de datos se encarga de seleccionar y transformar los datos para prepararlos para el proceso,
• El analista de dominio es un experto que puede analizar los resultados para validarlos.

En algunos procesos KDD, solo se hace referencia al usuario, lo que implica que el usuario cumple varios roles ⁽³⁾.

La tarea representa la meta u objetivo de un proceso KDD.

En la práctica, se distinguen dos grandes familias de tareas realizadas en KDD: descripción y predicción ⁽⁵⁾.

• La descripción se centra en la búsqueda de características generales relacionadas con los datos buscados, estos son patrones (modelos, diagramas o reglas) que describen estos datos, deben ser comprensibles e interpretables por el usuario,
• La predicción consiste en utilizar atributos de la base de datos para predecir valores futuros o desconocidos de otras variables.

Formalmente, la minería de datos se considera el paso central en el proceso KDD. Para ello, se utilizan algunos de los métodos previamente descritos.

Dentro de los métodos usuales que utiliza el KDD tenemos el agrupamiento, la estimación (K-means por ejemplo), la predicción (redes neuronales por ejemplo), la búsqueda de asociaciones, el análisis de excepcionalidades y desviaciones y los procesos de visualización (selección de subespacios, planeación y herramientas gráficas). Por razones de extensión no se profundizará en cana una de ellas.

Las fases del Proceso KDD son: Selección de datos, preprocesamiento (limpieza, transformación y reducción), transformación (agregación, generalización, normalización, adición de atributos), procesamiento, validación, evaluación y presentación.

Una de las fases más importantes es la de validación. Esta puede realizarse en forma estadística o por experiencia. La primera se ejecuta mediante técnicas de la estadística clásica y la segunda mediante pares expertos en el área problema.

Estos expertos juzgarán la relevancia de los resultados producidos. Por ejemplo, en el campo médico, la razón extraída debe ser fácil de entender; para ello, una primera validación debe ser realizada por un perito médico que juzgará antes la comprensibilidad del motivo.

La validación completa de un sistema basado en KDD se trata entonces de asegurar la adecuación entre el conocimiento modelado en la base de conocimiento y el conocimiento del experto, este es el paso esencial de un proceso clínico-matemático integrador que nosotros llamamos arquitectura biodigital ⁽⁷⁾.

Debido a la importancia de la validación de expertos para los métodos de minería de datos, así como los de analítica incluyendo el KDD, se describirán los principales métodos para la misma.

a. Validación mediante el examen de los resultados obtenidos de la base de conocimientos: Permite medir la adecuación entre el conocimiento real y su modelado comparando los resultados del sistema y los del experto en un conjunto de problemas que constituyen un conjunto de pruebas.

En este tipo de validaciones, se asume que el experto tiene una descripción del mundo real en forma de un conjunto de problemas característicos acompañados de sus soluciones.

Para este tipo de validación, se utilizan muchos métodos, como retención, submuestreo aleatorio, validación cruzada y Bootstrap ⁽⁸⁾.

Sin embargo, las métricas de rendimiento se pueden utilizar para analizar modelos predictivos. Se basan en cuatro valores de la matriz de confusión resumidos como verdadero positivo (TP), falso positivo (FP), verdadero negativo (TN) y falso negativo (FN).

Además, en otro nivel de verificación, la evaluación del rendimiento de toda la prueba se estima mediante la tasa de error y se calculará utilizando medidas de error comunes. Por lo tanto, se utiliza sensibilidad (sensibilidad) y especificidad (precisión).

b. Validación mediante el estudio de la consistencia de la base de conocimientos.

La detección de inconsistencias en una base de conocimiento supone que se da en un modelo conceptual del mundo real para el estudio de la consistencia.

Este modelo puede considerarse más explícito que el conocimiento resultante de la base de conocimientos. Con la ayuda de este modelo, podemos juzgar la consistencia de la base de conocimientos sin recurrir a un experto.

Aplicaciones en la gestión de la decisión médica

Campos de acción de la minería y analítica de datos en medicina

La medicina se ha volcado hacia la minería de datos debido a la inmensa cantidad de datos acumulados a lo largo de los años en grandes bodegas.

Por lo tanto, la contribución de la minería de datos en medicina ha sido sustancial, principalmente a través de la provisión de herramientas específicas para analizar datos médicos para el apoyo a la toma de decisiones ⁽⁹⁾.

Además, resulta fascinante encontrar relaciones interesantes entre entidades, como el vínculo que puede existir entre la toma de un fármaco y un efecto secundario, para deducir los efectos adversos de este. Por lo tanto, la minería de datos ha resultado ventajosa en muchos estudios y sistemas de apoyo al razonamiento clínico en diferentes esferas a saber:

En el diagnóstico

La búsqueda de pacientes que puedan ser sometidos a regímenes terapéuticos bien definidos es una de las primeras aplicaciones para estos métodos. La categorización de pacientes se realiza para orientar a los pacientes por grupos.

La búsqueda de factores de riesgo para patologías específicas como el cáncer se realiza a partir de datos de estudios epidemiológicos, con la elección de un tratamiento adecuado e individualizado. Con esta idea, Mokeddem presentó un nuevo enfoque para el diagnóstico de la enfermedad coronaria, este nuevo método se basa en algoritmos genéticos y la clasificación bayesiana ⁽¹⁰⁾.

En el tratamiento

La asociación de fármacos con sus efectos secundarios en una categoría de pacientes es una tarea que se abordó muy temprano en la minería de datos médicos [Prather y colaboradores, 97]. También se abordó la búsqueda de una asociación entre el tratamiento y una sintomatología determinada, seguida de un estudio sobre los efectos adversos ⁽¹¹⁾.

Por ejemplo, en la predicción de enfermedad cardiovascular en un paciente determinado ⁽¹²⁾.

Algunos médicos necesitan seguir las categorías de los pacientes para promover los tratamientos más apropiados para ellos ⁽¹³⁾.

En la predicción clínica

Actualmente existen múltiples modelos de este tipo. Localmente, por ejemplo, usamos una red neuronal para la predicción de la supervivencia de pacientes con cáncer de pulmón de células no pequeñas avanzado, en una institución colombiana, y otro modelo similar para estimar la supervivencia en pacientes con este mismo diagnóstico, pero con mutación en el gen EGFR ⁽¹⁴⁾.

Logette y colaboradores desarrollaron un modelo de predicción por machine learning respecto a niveles de glucosa en suero y progresión en la severidad de Covid-19 ⁽¹⁵⁾.

Luo y colaboradores, usaron modelos de DL/ML con procesadores de lenguaje natural para predecir pacientes con síntomas crónicos, en su caso tos a partir de datos estructurados y no estructurados ⁽¹⁶⁾.

En la hipercomplejidad

Una gran parte de los problemas de decisión se caracteriza por la diversidad de puntos de vista que a menudo son contradictorios y miden las cosas de manera diferente.

Además, hay muchas situaciones concretas en las que las consecuencias son lo suficientemente complejas como para que una sola función objetivo (un solo criterio) no pueda capturar toda la información necesaria para la comparación global de acciones (soluciones).

La resolución de este tipo de problemas debe tener en cuenta simultáneamente todos los puntos de vista que el decisor considere relevantes y varios criterios: este es el análisis multicriterio (MCDA).

A finales de los años sesenta nació este paradigma, que aglutina gran parte de las nociones de optimización de criterio único.

Los investigadores en este nuevo modo de razonamiento están desarrollando nuevas formas de trabajar para resolver problemas de toma de decisiones de un nuevo tipo que son diferentes al paradigma de criterio único. S

in embargo, surgen nuevas preguntas, sobre el cómo sopesar los criterios y cómo agregarlos. De hecho, el paradigma multicriterio se caracteriza por un patrón de pensamiento que considera varios criterios que deben ser considerados en el proceso de toma de decisiones.

Este paradigma encuentra su justificación en la observación que es muy difícil, si no imposible, optimizar todos los puntos de vista desde los que el decisor toma su decisión.

A partir de ahí, intentamos desarrollar modelos más o menos formalizados para mejorar, facilitar y apoyar al tomador de decisiones en todo el proceso de toma de decisiones.

Todos los métodos y modelos desarrollados en análisis multicriterio tienen un objetivo común que es ayudar al decisor a elegir que le satisface e integrarlo en un proceso de toma de decisiones, ofreciéndole la posibilidad de avanzar hacia una solución ⁽¹⁷⁾.

Un problema clínico de decisión de criterio único es usualmente de este tipo:

Optimizador= {g (x) : x ∈ A} donde:
A es el conjunto de acciones admisibles y
g es la función de criterio para optimizar.

Este modelo generalmente refleja un problema bien estructurado y matemáticamente bien definido, que se impone tanto al tomador de decisiones como al alumno, por ejemplo:

Optimizador= {Price (x) : x ∈ A}

Cuando las acciones potenciales de un problema de decisión no son evaluadas por un solo criterio, sino por un conjunto de criterios denotados por g¹ , g² …, gⁿ  , y que el tomador de decisiones desea optimizar simultáneamente, el problema presentado entonces será uno de la siguiente forma:

Optimizador= {g1 (x), g2 (x),… gm (x) : x  ∈ A}

La principal dificultad de un problema multicriterio es que es un problema sin una solución objetiva. En general, no hay acción mejor que todas las demás, y simultáneamente en todos los criterios. El concepto de solución óptima, un postulado básico del enfoque de criterio único, por lo tanto, no tiene sentido en un contexto de criterios múltiples. Por lo tanto, se trata de ayudar al tomador de decisiones a avanzar hacia una acción de compromiso ⁽¹⁸⁾.

Pero las decisiones clínicas distan mucho de ser simples, por lo que aparecen como una multiplicidad múltiple, por lo que vamos a abordar este problema desde el análisis multicriterio.

Dada la complejidad de las diversas situaciones en las que los seres humanos están llamados a decidir, se proporcionan uno o más criterios en un entorno a veces aleatorio.

El decisor no puede evaluar correctamente un problema para solucionarlo, sobre todo si entran en juego varios parámetros para evaluar la situación y decidir una acción (solución), lo que significa que el tomador de decisiones elige el análisis multicriterio porque el tomador de decisiones no puede hacer una evaluación teniendo en cuenta varios parámetros a veces contradictorios. Esto “va más allá” de estas capacidades mentales.

Sin embargo, recurre a la MCDA para que le ayude a hacer esta “combinación” de opciones utilizando métodos probados y puede proporcionar cálculos combinatorios o, a veces, recursivos para obtener la mejor opción.

Entonces, el objetivo es encontrar la solución óptima si podemos decir los siguientes parámetros: el problema, las respuestas esperadas y los criterios de evaluación en los que se basa para encontrar una solución ⁽¹⁸⁾.

El Paradigma Multi-Criterio

Muchos enfoques abordan problemas de decisión. Las técnicas clásicas (utilidad, teoría de juegos, análisis costobeneficio, programación matemática, etc.) han ayudado a abordar problemas de decisión optimizando un objetivo (costo, distancia, etc.).

La ayuda para la toma de decisiones de criterios múltiples pareció abordar varios problemas de decisión (elección, clasificación, orden, etc.) utilizando criterios y las preferencias de los tomadores de decisiones. Este enfoque procede tanto del uso de un enfoque junto con otros métodos prácticos para resolver los problemas de decisión, entre ellos:

El de la acción

Es una representación del elemento de solución que contribuye a la decisión; por ejemplo, la compra de un producto determinado o la elección de un sitio para construir una clínica constituyen acciones. Cuando las acciones son exclusivas, usamos el término “variante”. El propósito de las acciones potenciales es delimitar el campo de posibles soluciones.

Podemos mostrar dos tipos de acciones potenciales: acciones reales y acciones ficticias. El primero corresponde a una realidad que el tomador de decisiones puede comprender; por ejemplo, un tratamiento con osimertinib es una acción real. Sin embargo, es posible que queramos considerar medidas que no se correspondan con ninguna realidad existente pero que nos permitan informar decisiones; son acciones ficticias.

Estas servirán de base para realizar comparaciones. Si nos mantenemos en la industria farmacéutica, podemos decir que un “tratamiento contra el cáncer” o un “medicamento para el carcinoma de células no pequeñas” son acciones ficticias.

El del criterio

Schärlig propone la siguiente definición para lo que conocemos como criterio: “Es un punto de referencia contra el cual se mide la consecuencia de una acción, en otras palabras, un criterio expresa más o menos las preferencias del tomador de decisiones en relación con un atributo dado” ⁽¹⁹⁾.

Una sola acción puede contribuir al mismo punto de vista. Por ejemplo, un automóvil de clase A se puede definir como el medio para modelar un punto de vista.

Sin embargo, varios aspectos desde la perspectiva de la comodidad de un automóvil deben considerar diversos aspectos como la suspensión, el agarre a la carretera, el nivel de ruido, etc.

Un criterio es entonces una función g definida sobre A y que toma sus valores en un conjunto R completamente ordenado, donde g: A → R, y que representa las preferencias del decisor según el punto de vista. Luego distinguimos varios tipos de criterios: el criterio verdadero, el pseudo criterio, el cuasi criterio.

Por tanto, cada acción a de A estará representada por un vector (gl (a), …, Gn (a)) al que llamamos vector de rendimiento. El conjunto A de acciones estará representado por una matriz denominada matriz de desempeño. Por tanto, estas existen en diferentes tipos de criterios: el criterio real, el pseudocriterio, el cuasicriterio y el precriterio.

El de los pesos ponderales

En el análisis multicriterio, es bastante común que el tomador de decisiones piense que un criterio es más importante que otro por varias razones, incluidas las preferencias personales. Llamamos ponderación o peso ponderal (w) al concepto que mide la importancia relativa entre criterios tal como los ve el tomador de decisiones. Sin embargo, esta medida no siempre la determina fácilmente quien toma las decisiones. Deben reflejar los puntos de vista de los diferentes actores involucrados en la toma de decisiones. Este último “se basa en un sistema de diferentes percepciones, valores y opiniones para explicar sus preferencias. En varios métodos de ponderación, algunos criterios pueden influir en gran medida en el resultado final del análisis. (Eastman y colaboradores)

Una de las mayores dificultades que se encuentra en la resolución de problemas de criterios múltiples es asignar ponderaciones a diferentes criterios que conducen a la toma de decisiones, especialmente cuando el número de criterios es suficientemente alto ⁽²⁰⁾.

Por las dificultades anteriores, los decisores usualmente deben migrar a construir matrices de desempeño. En este tipo de matrices, para cada acción considerada y para cada criterio, se estima un umbral de preferencia (p), indiferencia (q) y un umbral de veto (v).

A cada criterio se le asigna un peso (w) que refleja su contribución a la decisión final. Los resultados del análisis de consecuencias se presentan en una matriz de desempeño, también llamada matriz de evaluación o matriz de juicio.

El problema puede verse como una orientación de la investigación que se adopta para un problema de decisión particular. Expresa los términos en los que el decisor o investigador plantea la pregunta y traduce el tipo de solución que desea obtener. Es posible distinguir tres preguntas básicas, cuyas características se resumen a continuación. Por tanto, cualquier problema de toma de decisiones multicriterio debe necesariamente reducirse a una de ellas, luego tenemos los problemas de: elección, clasificación, arreglo y descripción, respectivamente, anotados, Pa, Pb, Pg y Pd ⁽²¹⁾.

Problema de elección (Pα)

Consiste en seleccionar un subconjunto lo más pequeño posible del conjunto de acciones A, que contiene las mejores acciones. Lo ideal es conseguir una mejor acción. Pero debido a la naturaleza conflictiva de los criterios, es mejor proporcionar al tomador de decisiones algunas acciones que representen diferentes variaciones de la “mejor acción”. Formalmente, el resultado de este tipo de situación de toma de decisiones es un subconjunto A. Ejemplo: elegir la mejor ruta para que una ambulancia llegue al hospital.

Problema de clasificación (Pβ)

Consiste en asignar cada acción a un conjunto de categorías predefinidas.

Esta formulación es adecuada cuando el problema de decisión consiste en examinar cada acción de forma independiente de las demás (teniendo en cuenta solo las características intrínsecas de cada acción) para proponer una recomendación entre un conjunto de recomendaciones previamente especificadas. Cada recomendación se puede asociar a una categoría.

El problema de decisión se ve entonces como la clasificación de acciones potenciales en diferentes categorías predefinidas. El procedimiento de clasificación debe definirse de manera que cada acción se asigne a una y solo una categoría. Por ejemplo, la asignación de cada ambulancia es una acción, a una emergencia particular entre diferentes emergencias (ambulancia básica Vs medicalizada Vs pediátrica) para accidente cerebrovascular agudo, politraumatismos o infección Covid-19.

Problema de almacenamiento (Pγ)

Consiste en ordenar las diferentes acciones desde la mejor acción hasta la más deficiente, con un posible empate. Este problema es interesante cuando las acciones deben diferenciarse según su interés relativo. Cabe señalar que, en la práctica, el almacenamiento puede ser necesario solo para las acciones más interesantes: por ejemplo, la diferenciación de instituciones según la especialidad comenzando por el sitio más experimentado o el más cercano.

Problema de descripción (Pδ)

Simplemente consiste en describir las acciones y sus consecuencias y no compararlas como con los otros tres temas anteriores. Aquí no hay solución. Ejemplo: identificar y describir, con el único propósito de aprender y prepararse para posibles incidencias.

Para la formulación multicriterio de un problema de decisión de elección el tomador de decisiones utilizará diferentes acciones (posibles soluciones), criterios y ponderaciones para estos. Por tanto, un problema multicriterio se definirá de la siguiente manera:

Problema de decisión multicriterio (Ap, Ck, Wt)

Donde: A = {a¹ , a² ,. . ., aⁿ },
el conjunto de acciones potenciales (o alternativas).
C = {c¹ , c² ,. ., cᵐ},
los criterios de evaluación (cj)
(ai) = evaluación de ai según el criterio cj).
W = {w¹ , w² ,. . ., wᵏ },
las ponderaciones de los criterios.

Este problema de toma de decisiones multicriterio estará representado por una matriz de juicio que representará la evaluación cuantitativa o cualitativa de los diferentes criterios que entrarán en la búsqueda de la solución de “apoyo a la toma de decisiones”.

Existen diferentes enfoques para llevar a cabo una situación de decisión multicriterio. Cada enfoque enfatiza algunos aspectos a expensas de otros y, por lo tanto, cada uno tendrá sus ventajas y desventajas. Hay dos enfoques dependiendo de la escuela elegida para este efecto:

a. La escuela americana basada en el enfoque de arriba hacia abajo (“up and down”) de los objetivos que establece ⁽¹⁸⁾.

b. La escuela francesa se basa en el enfoque de abajo hacia arriba (de “bottom-up”) ⁽¹⁸⁾ y consiste en construir una estructura jerárquica que tiene en su primer nivel el objetivo general que se “descompone” en subobjetivos que, a su vez, se “desglosan” en subobjetivos hasta formar un grupo medible denominado atributos ⁽¹⁸⁾.

En cuanto al enfoque “bottom-up” de Roy, este identifica todas las consecuencias resultantes de la implementación de acciones, que se estructuran en dimensiones y luego en ejes de significado en torno a los cuales se construyen los criterios [Roy, 85]. Chakhar aclara que: “Los métodos de apoyo a la decisión desarrollados bajo el primer enfoque son muy diferentes de los desarrollados bajo el segundo enfoque, pero no entran en conflicto porque se aplican a diferentes problemas. Por lo tanto, son bastante complementarios” ⁽²²⁾.

Según Vansnick, “ambas escuelas se basan en el mismo modelo de decisión para la aplicación de sus métodos” ⁽²⁰⁾.

Los problemas de decisión de criterios múltiples normalmente operan en tres fases. Ben Mena señala que los dos primeros son comunes para todos los métodos multicriterio, a diferencia de los dos últimos que dependen del método elegido. Se propone el siguiente enfoque ⁽¹⁷⁾:

1. Crear una lista de posibles acciones.

Durante este paso, establecemos una lista de acciones potenciales que competirán. Esta lista no es exhaustiva ni definitiva. Puede cambiar a lo largo del estudio (eliminación o adición de acciones).

2. Modelar las preferencias del tomador de decisiones (Creación de una matriz de desempeño).

– Creación de una lista de criterios para tener en cuenta. Se trata de desarrollar la lista de criterios a considerar. Un criterio puede ser más importante que otro. Esta importancia relativa se expresa en pesos ponderales.

– Evaluar las acciones según los criterios y crear la matriz de desempeño. Cualquier método multicriterio actúa sobre la matriz de desempeño. Se trata de juzgar cada acción según cada uno de los criterios; esta es la matriz de desempeño. Es de dimensión (n × m) que, para cada acción A1 de el conjunto de acciones A, hacemos coincidir un vector G = (G¹ (A¹ ), G² (A¹ ),…. Gⁿ (A¹ )). Estos valores numéricos a menudo se denominan beneficios. Se consideran dos conjuntos; la primera A es la de acciones, la segunda C es la de criterios:

A = {A¹ , A² , A3 …. Aⁿ⁰};
C = {C¹ , C² , C3 … Cᵐ},

donde n es el número de acciones y m es el número de criterios. Sij denota el desempeño o evaluación de la acción Ai contra el criterio Cj.

3. Agregación de preferencias

Para definir una solución para la agregación -una acción que genera una preferencia común con las mejores calificaciones globales-, los juicios deben ser agregados; esto se denomina agregación de preferencias que consiste en “una operación que permite obtner información sobre la preferencia general entre potenciales de acción, a partir de información sobre preferencias de criterios.

Se trata de establecer un modelo de preferencias globales. Esta representación formaliza dichas preferencias en relación con un conjunto A de acciones potenciales que el investigador considera adecuadas al problema de las ayudas.

Por lo tanto, un problema de criterios múltiples manejará un conjunto denotado A {aⁱ , a² ,… … aⁿ } donde ai es la acción i.

Las acciones se evalúan y comparan sobre la base de un conjunto de criterios de evaluación g¹ , g² ,…, gᵐ. La evaluación de una acción a según un criterio gj se escribe gj (a).

Entonces definir una solución (acción) que genere una preferencia común (que generalmente disfruta de las mejores evaluaciones), juicios o evaluaciones parciales (es decir, por cada criterio) debe agregarse en una evaluación general utilizando un mecanismo de agregación apropiado.

Esta agregación consiste en utilizar un mecanismo de agregación matemática para combinar las distintas evaluaciones parciales (es decir, en relación con cada criterio) en una evaluación global (es decir, que tiene en cuenta todos los criterios).

Los procedimientos de agregación son, en cierto modo, la principal característica de los métodos multicriterio. Los métodos multicriterio difieren según sus formas de manejar esta operación (agregación).

Actualmente estamos explorando un nuevo enfoque que utiliza Ecosistemas Médicos Digitales (DME) para la integración y un Reasoner (apoyo a la decisión basado en caso -por ejemplo, por tipo de cáncer o por marcador biológico- y un razonador de caso) para proporcionar una estrategia de recuperación que, en última instancia, nos permite elegir la mejor solución entre un conjunto de situaciones ya resueltas.

Este enfoque ayudará a abordar ciertas desventajas vinculadas al hecho de encontrar varios casos similares y, en consecuencia, varias soluciones más o menos aceptables. Utilizamos un modelo de toma de decisiones basado en la idea de integrar dos modos de razonamiento que pueden ser complementarios. Este método de agregación es útil para escenarios clínicos que tienen múltiples elecciones con similares niveles de evidencia científica o por ejemplo para optimizar las matrices de valor terapéutico como la ESMO-MCBS.

El DME permite la integración de la información que surge de la mera tramitación de la cita médica, en la que la historia clínica electrónica (HCE) registra una pequeña fracción de lo que implica la asistencia sanitaria. Un DME es un conjunto de información que captura desde donde se produce la información relacionada con la salud y la salud efectiva en la vida real de un paciente.

Definimos la situación médica (caso) en el que el médico generalmente está en consulta con un paciente y tendrá que explorar el posible diagnóstico para prescribir el mejor tratamiento, guiado por esta definición y por las nociones que hemos planteado, a saber:

Un razonamiento clínico y una toma de decisión para la situación. El caso médico que recomendamos lo describe el tomador de decisiones (médico) antes de diagnosticar a un paciente y debe explorar posibles soluciones (diagnóstico(s)) para elegir el mejor tratamiento.

Por tanto, la situación médica se caracteriza por una definición más o menos completa del problema, un estudio exhaustivo de los posibles diagnósticos, tratamientos y la existencia de preferencias individuales para cada diagnóstico o tratamiento.

Además, la presencia de signos específicos para cada paciente, por ejemplo, “anciano frágil”, “alergia a la penicilina”, etc.

Estos signos específicos guiarán o indicarán el tratamiento deseado (por ejemplo, un paciente anciano puede ser menos capaz de seguir una dieta hipersódica). Además, hoy en día se reconoce ampliamente que las decisiones diagnósticas relacionadas con cada paciente deben tener en cuenta el contexto relativo definido a través de los signos específicos.

Así, el médico determina una situación patológica con sus síntomas clínicos y v signos específicos. Desde el punto de vista de la modelización, la situación médica se convierte en un problema médico definido por descriptores y una solución considerada de “diagnóstico / tratamiento”. Para formalizar esta situación médica utilizamos la siguiente estructura:

Situación médica = {síntomas clínicos, signos específicos, diagnóstico / tratamiento propuesto}

La integración parte de la idea de poner en común el DME y los procedimientos Reasoner para apoyar al DME en su búsqueda de situaciones similares o cercanas a la situación actual de toma de decisiones.

En el nivel operativo de este DME y la integración del razonador, al razonador se le asigna la tarea principal de “reducir todos los casos elegibles a la solución correcta para lograr la solución”.

De lo contrario, cada razonador integra sus funcionalidades, sus proios datos sobre la situación médica y su interfaz para comunicarse con el usuario “médico”.

La integración entre ellos se realiza mediante un bloque que actúa como puente. Permite el intercambio de datos de forma que se adapte a las dos partes del DME y el razonador, que cooperarán en la búsqueda de la mejor solución (Diagnóstico / Tratamiento) + Seguimiento ambulatorio.

Nuestro enfoque se basa en aplicar una estrategia de integración para lograr un “mejor” soporte de decisiones. Para ello, hemos utilizado el siguiente procedimiento:

1. Definir la situación médica,
2. Iniciar el DME (para nuestro caso MAIA ®),
3. Llamar al razonador para orientar la búsqueda de una solución e intercambiar datos con este,
4. Proponer una solución,
5. Si se acepta la solución, se registra la nueva situación médica con una solución para su uso posterior; de lo contrario, el tomador de decisiones puede volver a una etapa anterior para revisar su situación médica o revisar una etapa particular del proceso actual.

El modelo necesario para establecer una estrategia de solución para una situación médica, debe definir algunos elementos esenciales que apoyan esta situación para describirla mejor desde el principio y continuar el camino hasta alcanzar el objetivo de establecer el apoyo a las decisiones médicas.

La definición de la situación médica (caso) es la comprensión y percepción de la situación. El médico analiza el contexto de la situación y define los objetivos de la decisión.

Así, el médico define su situación médica. Para ellos usa el análisis de síntomas clínicos (Cs) y signos específicos (Ss). Luego puede sugerir un posible diagnóstico / terapia que será considerado como una elección para la situación en cuestión, la cual se basa en la valoración personal del médico (tomador de decisiones), sin que esta opinión médica sea una solución en esta etapa.

Este procedimiento es utilizado por los dos ejes del modelo de toma de decisiones: Ecosistema Médico Digital y Razonador. Por tanto, este procedimiento incluye la definición del nuevo caso del Ecosistema Médico Digital y la definición del problema médico por parte del razonador.

Este modelo decisional apoyará el procesamiento representado en la Figura 2.

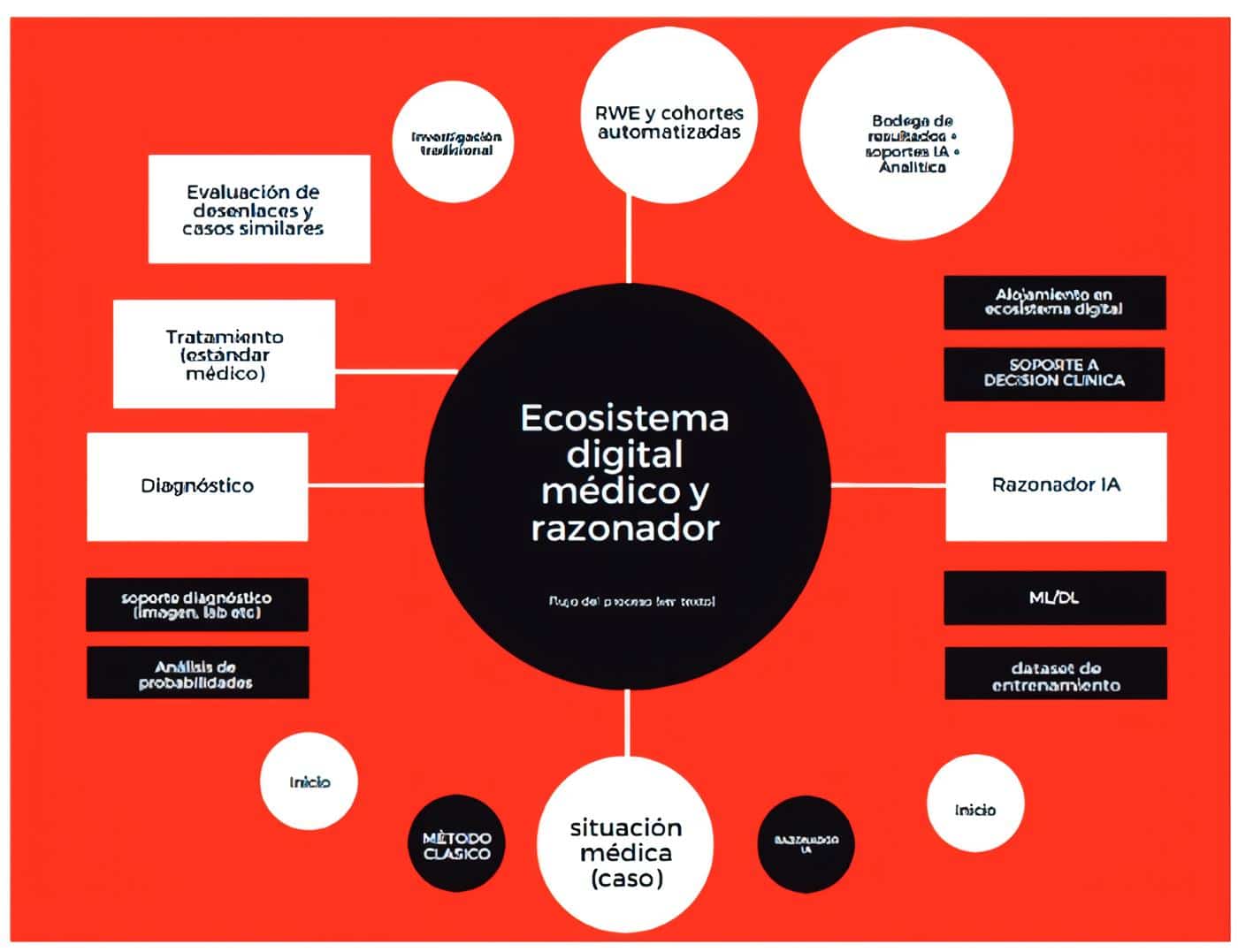
Figura 2. Ecosistema médico digital y razonador (elaboración propia).

Conclusiones – Encuentro entre la Medicina y la Matemática

La intersección entre la complejidad de los datos biológicos y clínicos requiere un enfoque matemático que vaya mucho más allá de la epidemiología clásica para optimizar no solo las decisiones clínicas, sino también para integrarlas en un ambiente de optimización que permita la consolidación de la medicina de precisión no solo en dianas terapéuticas sino también en la validación de datos que hace que los desarrollos posteriores de la IA sean realmente un elemento mucho más médico que tecnológico.

En este capítulo no se abordó el concepto de la biología de sistemas, una ciencia en evolución que integra modelos mecanicistas medicina y matemática ⁽²³⁾.

Se escribirá sobre ella en el futuro.

Referencias – Encuentro entre la Medicina y la Matemática

1. Hewitt P. Bernoulli´s Principle.Sci Teach. 2014;7(1):51- 55.
2. Dunham M. Data Mining: Introductory and Advanced Topics. Pearson Education; 2006.
3. Fayyad M, Smyth P, Piatesky-Shapiro G. From Data Mining to Knowledge Discovery. En Fayyad M, Smyth P, Piatesky-Shapiro G. From Data Mining to Knowledge Discovery.: Springer; 1996. p. 34.
4. Rossenblatt F. The perceptron: a probabilistic model for information storage and organization in the brain. Psychol Review. 1958;65(6):386-408.
5. Han JK, Pei J. Data mining, concepts and techniques. En Han JK, Pei J. Data mining, concepts and techniques; 2000.
6. Espinosa O., Rodríguez J., Robayo A, Arias L., Moreno S., Ospina M, et al. Vulnerability interactive geographic viewer against COVID-19 at the block level in Colombia. Reg Sci Policy. 2021;1.
7. Pino L. MAIA como plataforma integradora de salud usando arquitectura biodigital. [MBA].: EAN; 2019.
8. Broniatowski M. Minimum Divergence Indicators, Maximum Likelihood and Generalized Bootstrap. Entropy. 2021; 23(2):185.

Bibliografía – Encuentro entre la Medicina y la Matemática

9. Pelaccia T., Forestier G., Wemmert C. Deconstructing the diagnostic reasoning of human vrsus artificiL Intelligence. CMAJ. 2019;191(48):E1332-E1335.
10. Mokeddem S., Atmani B., Mokaddem M. A new approach for CAD diagnosis based on a genetic algorithm. Int J Decis Support Syst Techn. 2014;6(4):1-15.
11. Prather J., Lobach D., Goodwin L., Hales JW., Hage M., Hammond WE.. Medical data mining : Knowledge discovery in a clinical data warehouse. Proc AMIA Annu Fall Symp. 1997;101-105.
12. Pogdorelec V, Hericko M, Rozman I. Improving mining of medical data by outliers prediction. 18 ed. IEEE Symposium on Computer-Based Medical Systems(CBMS); 2005.
13. Ramírez J., Cook D., Peterson D. An event set approach to sequence discovery in medical data. Intell Data Anal. 2000;4(6):513-530.
14. Pino L., Triana I., Mejía J., Camelo M., Galvez-Nino M., Ruiz R, et al. Predictive Analytics in Real-World Data from Peru: The New Models for Personalized Oncology. JThorac Oncol. 2021;16(3):S294.
15. Logette E., Lorin C., Favreu C., Oshurko E., Coggan J., Casalegno F., Francois M, et al. A Machine-Generated View of the Role of Blood Glucose Levels in the Severity of COVID-19. Front Public Health. 2021;9:695139.
16. Luo X., Gandhi P., Zhang Z., Shao W., Han Z., Chandrasekaran V., Turzhitsky V, et al. Applying interpretable deep learning models to identify chronic cough patients using EHR data. Comput Methods Programs Biomed. 2021;210:106395.

Lecturas Recomendadas – Encuentro entre la Medicina y la Matemática

17. Benmena S. Introduction aux methods multicriteries dáide a la decision. Biotechnol Agron Environ. 2000;4(2):83- 93.
18. Keeney R, Raiffa H. Decisions with multiple objectives: preferences and value trade-offs. Cambridge University Press. 1993;.
19. Scharlig A. Décider sur plusieurs critères, panorama de l’aide à la décision multicritère. Collection Diriger l’entreprise. Presses Polytechniques et Universitaires Romandes; 1985.
20. Bana e Costa C. Readings in Multiple Criteria Decision Aid. En: Vansnick JC. Ed.Measurement theory and and decision aid.1ra ed. Berlín: Springer; 1990. p. 81-100.
21. Roy B. Méthodologie Multicritères d’Aide à la Décision. París: Economica. 1985.
22. Chakhar S. Cartographie décisionnelle multicritères: formalisation et implémentation informatique. Paris: Université Paris Dauphine; 2006.
23. Vodovotz Y. Integrating mindsets and toolsets at the frontiers of sistems biology. Front Syst Biol. 2021;1.

Autores – Encuentro entre la Medicina y la Matemática

---

1 Jorge Andrés Mejía Rubio , Luis Eduardo Pino V. MBA, MSc Finance. MAIA Healthcare y MedzAIo, Bogotá, Colombia
2 Luis Eduardo Pino V. MD, MSc, MBA. Miembro Fundador de AIpocrates. Departamento de Oncología Clínica, Instituto de Oncología, Fundación Santa Fe de Bogotá, Colombia.

Recibido: 12 de Noviembre, 2021
Aceptado: 22 de Noviembre, 2021

Correspondencia:
Luis Eduardo Pino V.
docpino2@gmail.com