Pruebas Diagnósticas: Razones de Probabilidad

Diagnostic Tests: Probability Ratios

Resumen

La utilidad de una prueba diagnóstica se cuantifica mediante el cálculo de las medidas de probabilidad y las medidas de razones de probabilidad.

Las medidas de probabilidad son la sensibilidad, la especificidad, valor predictivo positivo y el valor predictivo negativo.

La sensibilidad y la especificidad se usan para escoger la mejor prueba a utilizar, entre varias disponibles; sin embargo, no pueden ser utilizadas para estimar la probabilidad de determinada enfermedad en un paciente en particular.

En la práctica clínica es esencial saber cuál es la probabilidad de que un paciente con un resultado positivo en una prueba diagnóstica presente la enfermedad y cuál es la probabilidad de que un paciente con un resultado negativo en una prueba diagnóstica no presente la enfermedad.

Los valores predictivos positivos y negativos nos brindan la respuesta a esta cuestión, sin embargo, dependen tanto de la sensibilidad y especificidad, como de la prevalencia de la enfermedad en la muestra del estudio.

Las medidas de razones de probabilidad también describen el rendimiento o utilidad de una prueba diagnóstica y poseen dos propiedades importantes: resumen el mismo tipo de información que la sensibilidad y la especificidad, y pueden utilizarse para calcular la probabilidad de la enfermedad después de una prueba positiva o negativa.

El propósito de esta publicación fue definir el concepto de razones de probabilidad, exponer sus principales fortalezas y explicar cómo se calculan las razones de probabilidad cuando la prueba de interés expresa sus resultados en forma dicotómica, en más de dos categorías o de forma ordinal.

Palabras clave: diagnóstico; técnicas y procedimientos diagnósticos; prueba de laboratorio; probabilidad; razón de verosimilitud.

Abstract

The usefulness of a diagnostic test is quantified by calculating the probability measures and the probability ratio measures.

Probability measures are sensitivity, specificity, positive predictive value, and negative predictive value. Sensitivity and specificity are used to choose the best test to use, among several available; however, they cannot be used to estimate the probability of a certain disease in a particular patient.

In clinical practice it is essential to know what is the probability that a patient with a positive result in a diagnostic test will present the disease and what is the probability that a patient with a negative result in a diagnostic test will not present the disease.

The positive and negative predictive values provide us with the answer to this question, however, it depends both on the sensitivity and specificity, and on the prevalence of the disease in the study sample.

Probability ratio measures also describe the performance or usefulness of a diagnostic test and possess two important properties: they summarize the type of information that sensitivity and specificity, and they can be used to calculate the probability of disease after a positive or positive test. negative.

The purpose of this publication was to define the concept of probability ratio measures, expose its main strengths, and explain how probability ratio measures are calculated when the test of interest expresses its results dichotomously, in more than two categories or ordinally.

Keywords: diagnosis; diagnostic techniques and procedures; laboratory test; probability; likelihood ratio.

Introducción

La utilidad de una prueba diagnóstica se cuantifica mediante el cálculo de las medidas de probabilidad y las medidas de razones de probabilidad. Las medidas de probabilidad son la sensibilidad, la especificidad, valor predictivo positivo y el valor predictivo negativo.

La sensibilidad y la especificidad se usan para escoger la mejor prueba a utilizar entre varias pruebas diagnósticas disponibles, sin embargo, estas dos medidas no pueden ser utilizadas para estimar la probabilidad de determinada enfermedad en un paciente en particular.

En la práctica clínica usual, es esencial saber cuál es la probabilidad de que un paciente con un resultado positivo en una prueba diagnóstica presente la enfermedad, y cuál es la probabilidad de que un paciente con un resultado negativo en una prueba diagnóstica no presente la enfermedad.

Los valores predictivos positivo y negativo nos brindan esta información; sin embargo, ellos dependen de la prevalencia de la enfermedad en la muestra del estudio y rara vez pueden ser generalizados más allá del contexto del estudio.

Las razones de probabilidad proveen la solución a las limitaciones de los valores predictivos ya que ellas pueden ser usadas para calcular la probabilidad de la enfermedad en diferentes escenarios clínicos¹.

Las razones de probabilidad constituyen otra herramienta de gran valor que resumen la utilidad o rendimiento de una prueba diagnóstica. Las medidas de razón de probabilidad se conocen con otros nombres como: “razón de verosimilitud” (en español) y “likelihood ratio” (en inglés).

Definición de razones de probabilidad

Las medidas de razón de probabilidad se definen como cuántas veces más o cuantas veces menos probable es que se identifique un determinado resultado de una prueba en individuos enfermos comparados con los individuos sin la enfermedad ².

Es decir, una “razón de probabilidad” es la probabilidad de que una persona, que tiene la enfermedad, presente un resultado determinado en la prueba, dividido por la probabilidad de que un individuo sin la enfermedad presente ese mismo resultado 3.

Una de las grandes ventajas de recurrir a las razones de probabilidad como medida de utilidad de una prueba diagnóstica, es que se pueden utilizar cuando la prueba diagnóstica expresa sus resultados en forma dicotómica (positivo / negativo), en más de dos categorías o de forma ordinal.

Razones de probabilidad de una prueba a evaluar con resultados dicotómicos

Cuando el resultado de una prueba diagnóstica es dicotómico (prueba positiva o negativa) se pueden determinar dos tipos de razón de probabilidad: razón de probabilidad positiva (RPP) y razón de probabilidad negativa (RPN).

La sensibilidad y la especificidad de una prueba diagnóstica pueden ser combinadas para calcular las razones de probabilidad, de la siguiente manera ^4-6:

La fórmula para calcular la razón de probabilidad positiva (RPP) es:

RPP =       Sensibilidad     
             (1– Especificidad)

Donde el numerador de la razón de probabilidad positiva es la probabilidad o la proporción de verdaderos positivos, y el denominador es la probabilidad o proporción de falsos positivos.

Por el contrario, la razón de probabilidad negativa (RPN) es:

RPN =    (1– Sensibilidad)   
                   Especificidad

Donde el numerador de la razón de probabilidad negativa es la probabilidad o proporción de falsos negativos, y el denominador es la probabilidad o proporción de verdaderos negativos.

Al igual que la sensibilidad y la especificidad, las razones de probabilidad no se ven afectadas por la prevalencia de la enfermedad.

Interpretación de las razones de probabilidad

La razón de probabilidad positiva toma valores entre 1 y el infinito, mientras que la razón de probabilidad negativa toma valores entre el 1 y el cero.

Si la razón de probabilidad es igual a 1, la prueba es inútil, no tiene capacidad de catalogar a los enfermos como enfermos ni a los sanos como sanos. Cuanto más se alejen los valores de las razones de probabilidad de 1, mayor es el poder de la prueba diagnóstica para sacarnos de la zona de incertidumbre diagnóstica (tabla 1).

Tabla 1. Valores de las razones de probabilidad y su efecto en la utilidad clínica.

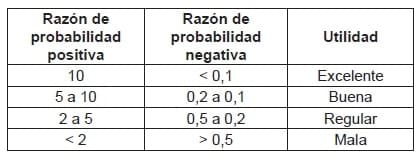
Una razón de probabilidad positiva mayor a 1 significa que un resultado positivo es más probable que ocurra en personas que tienen la enfermedad que en personas que no tienen la enfermedad.

Por otra parte, una razón de probabilidad negativa menor a 1 significa que un resultado negativo es menos probable que ocurra en personas que tienen la enfermedad que en personas sin la enfermedad.

Cálculo de razones de probabilidad positiva y negativa, a partir de la sensibilidad y especificidad de una prueba diagnóstica cuyos resultados son expresados en forma dicotómica: prueba positiva o prueba negativa.

La tabla 2 muestra los resultados de una revisión sistemática sobre el valor de la determinación de la ferritina sérica como prueba diagnóstica de la anemia ferropénica ⁷.

• Sensibilidad: a / (a + c) × 100 = 90 %.
• Especificidad: d / (b + d) × 100 = 85 %.
• Razón de probabilidad positiva: sensibilidad / (1-espeficidad) = 0,90 / 0,15 = 6
• Razón de probabilidad negativa: (1-sensibilidad) / especificidad = 0,10 / 0,85 = 0,12
• Prevalencia: 809 ÷ 2579 = 31 %.

Tabla 2. Diagnóstico por laboratorio de anemia ferropénica. Total pacientes estudiados: 2.579.

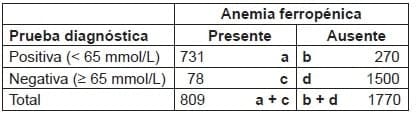
En este caso, la razón de probabilidad positiva es de 6, lo que significa que una prueba positiva es 6 veces más probable que ocurra en individuos con anemia ferropénica que en los individuos sin la anemia.

De otro lado, la razón de probabilidad negativa es 0,12, lo que significa que una prueba negativa es 0,12 veces menos probable que ocurra en individuos con anemia ferropénica que en los individuos sin la anemia.

Recordemos que una razón de probabilidad negativa menor a 1 significa que un resultado negativo es menos probable que ocurra en personas con la enfermedad que en personas sin la enfermedad.

Estimación de la probabilidad de la enfermedad

Toda hipótesis diagnóstica que se deriva de un proceso de análisis clínico (juicio clínico) lleva asociada una probabilidad de ocurrencia de la enfermedad denominada “probabilidad antes de la prueba” o “probabilidad pretest”.

Por ejemplo, si un paciente de 70 años, fumador, con obesidad e hipertensión arterial, presenta un dolor torácico retroesternal, opresivo, que se irradia al cuello, tendrá una probabilidad del 80 % de presentar un infarto del miocardio, según nuestro juicio clínico.

Esta probabilidad del 80 % se denomina probabilidad antes de la prueba. La probabilidad antes de la prueba no solamente puede ser estimada a través del juicio clínico sino también por los datos de la prevalencia de la enfermedad y publicaciones de reportes científicos.

La razón más importante por la cual los clínicos realizan una prueba diagnóstica es para tratar de obtener más información, la cual pueda modificar la probabilidad pretest.

La probabilidad del paciente de tener la enfermedad, después de que los resultados de una prueba diagnóstica sean conocidos se denomina “probabilidad postest” o “probabilidad posterior a la prueba”.

Los resultados de las pruebas diagnósticas no deben ser usados para, categóricamente, establecer o excluir un diagnóstico, sino para modificar la probabilidad pretest y generar la probabilidad posterior a la prueba diagnóstica ⁸.

En la práctica clínica, hay dos formas para estimar la probabilidad postest utilizando las razones de probabilidad: directamente, mediante el cálculo matemático, o usando el monograma de Fagan ⁸.

Cálculo matemático

Para calcular la probabilidad de la enfermedad, después de la aplicación de la prueba, seguimos los siguientes pasos.

Primero. Convertir la probabilidad antes de la prueba, en razón antes de la prueba, mediante la siguiente fórmula:

Segundo. Multiplicar la razón antes de la prueba o razón pretest, por la razón de probabilidad (positiva o negativa), para obtener la razón posterior a la prueba o razón postest.

Tercero. Convertir la razón postest, en probabilidad postest, mediante la siguiente fórmula:

                            Razón antes de la prueba =
                  =      Probabilidad antes de la prueba  
                          1– Probabilidad antes de la prueba

Ahora, utilizando las razones de probabilidad calculadas a partir de la tabla 2, podemos calcular la probabilidad postest, en pacientes en quienes se sospecha anemia ferropénica.

¿Cuál es la probabilidad posterior a la prueba de diagnosticar anemia ferropénica en un niño de 11 años con antecedente de parasitosis intestinal, actualmente con astenia, adinamia y palidez, si la ferritina sérica es de 40 mmol/l?

Acorde al juicio clínico, este paciente tiene una alta probabilidad de tener anemia ferropénica, digamos del 80 %. Esta probabilidad es la probabilidad antes de la prueba o pretest. Entonces, debemos seguir los mismos pasos:

Primero. Convertir la probabilidad pretest en razón pretest.

Resolviendo la ecuación, la razón pretest es igual a 0,80 / (1 – 0,80) = 0,80 / 0,20 = 4.

Segundo. Obtener la razón postest. La obtenemos multiplicando la razón pretest por la razón de probabilidad positiva, o sea, 4 × 6 = 24

Tercero. Convertir la razón postest en probabilidad postest.

       Probabilidad pos test =
=        Razón pos test       
      (Razón pos test + 1)

Resolviendo la ecuación, la probabilidad postest es igual a 24 / (1 + 24) × 100 = 96 %. Esto significa que la probabilidad de este niño de tener anemia ferropénica después de habérsele realizado la prueba de ferritina sérica pasó de un 80 % a un 96 %, lo que confirma el diagnóstico de anemia ferropénica.

Monograma de Fagan

Para obviar los cálculos matemáticos anteriores, se utiliza el monograma de FAGAN ⁹, para obtener la probabilidad postest a partir de la probabilidad pretest. En el monograma, la razón de probabilidad pretest y postest de la prueba, ya están convertidas en sus probabilidades correspondientes (figura 1).

Figura 1. Monograma de Fagan

El uso del monograma es muy simple: basta con colocar una regla en la probabilidad pretest que está a la izquierda, luego cotejamos la regla con la razón de probabilidad correspondiente, que está en el centro del monograma, y la alineamos con la probabilidad postest, que está a la derecha.

De esta manera fácil obviamos la necesidad de convertir entre probabilidades y razones de probabilidad.

En el caso de nuestro paciente de 11 años con impresión diagnóstica de anemia ferropénica, con un valor de ferritina sérica de 40 mmol/L, basta colocar una regla en 80 (probabilidad pretest), anclarla en la razón de probabilidad correspondiente (de 6) y alinearla con la probabilidad postest a la derecha, entonces obtenemos una probabilidad postest de 96 %.

Razones de probabilidad de la prueba de interés cuyos resultados esta expresados en una escala ordinal

Veamos ahora, cómo se calculan las razones de probabilidad cuando los resultados de una prueba diagnóstica se expresan en una escala ordinal, en vez de dos categorías.

Los datos de este ejemplo son tomados del estudio PIOPED ¹⁰, donde 251 pacientes tuvieron embolismo pulmonar comprobado por angiografía, mientras que en 630 pacientes se descartó el embolismo pulmonar por medio de la misma prueba.

La tabla 3 muestra los resultados de la gammagrafía de perfusión pulmonar para el diagnóstico de embolismo pulmonar. Los resultados de la gammagrafía de perfusión pulmonar fueron expresados como probabilidad para embolismo pulmonar alta, intermedia, baja y normal.

Tabla 3. Resultados de la gammagrafía de perfusión pulmonar (GPP) para el diagnóstico de embolismo pulmonar.

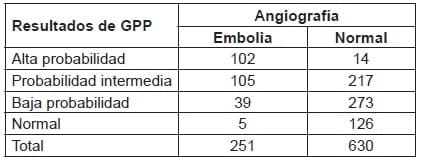
Cálculo de probabilidad para cada nivel de los resultados

¿Cómo calcular las razones de probabilidad para los resultados de la gammagrafía de perfusión para el diagnóstico de embolismo pulmonar?

Primero. Calcular la probabilidad para embolismo pulmonar para cada nivel de los resultados de la gammagrafía pulmonar, en los pacientes con embolismo pulmonar y en los pacientes sin embolismo pulmonar. La tabla 3.1 muestra estas probabilidades

 Tabla 3.1. Probabilidad para embolismo pulmonar para cada nivel de los resultados de la gammagrafía pulmonar, en los pacientes con embolismo pulmonar y en los pacientes sin embolismo pulmonar. 

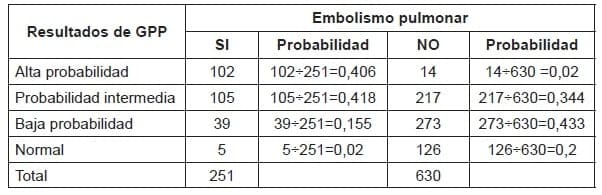
Segundo. Calcular la razón de probabilidad para cada nivel de los resultados de la gammagrafía pulmonar.

Recordemos que una razón de probabilidad es la probabilidad de que una persona que tiene la enfermedad presente un resultado determinado en la prueba, dividido por la probabilidad de que un individuo sin la enfermedad presente ese mismo resultado.

Por consiguiente, la razón de probabilidad para cada nivel de los resultados de la gammagrafía pulmonar se calcula dividiendo cada probabilidad de los pacientes con embolismo pulmonar entre los pacientes sin embolismo pulmonar.

La tabla 3.2 muestra las razones de probabilidad para cada nivel de los resultados de la gammagrafía pulmonar.

Se puede observar que, cuando el resultado de la GPP es de alta probabilidad, la razón de probabilidad es de 18,4; cuando es de probabilidad intermedia, la razón de probabilidad es de 1,21; cuando es de probabilidad baja, la razón de probabilidad es de 0,357, y cuando el resultado es normal, la razón de probabilidad es de 0,1.

Tabla 3.2. Razones de probabilidad para cada nivel de los resultados de la gammagrafía pulmonar.

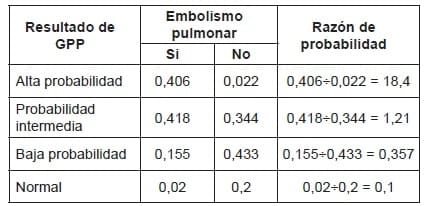
Si la razón de probabilidad es igual a 1, la prueba es inútil, no tiene capacidad de catalogar a los enfermos como enfermos y a los sanos como sanos.

Cuanto más se aleje de 1 el valor de la razón de probabilidad, mayor es el poder de la prueba diagnóstica para sacarnos de la zona de incertidumbre diagnóstica.

Estimación de la probabilidad de la enfermedad

Para calcular la probabilidad de la enfermedad, después de la aplicación de la prueba, seguimos los siguientes pasos.

Primero. Convertir la probabilidad pretest, en razón pretest, mediante la siguiente fórmula:

                Razón antes de la prueba =
=         Probabilidad antes de la prueba      
         1– Probabilidad antes de la prueba

Segundo. Multiplicar la razón antes de la prueba o razón pretest, por la razón de probabilidad, para obtener la razón posterior a la prueba o razón postest.

                   Razón pos test =
Razón pre test × Razón de probabilidad

Tercero. Convertir la razón postest, en probabilidad postest, mediante la siguiente fórmula:

         Probabilidad pos test
=           Razón pos test      
         (Razón pos test + 1)

¿Cuál es la probabilidad de que un paciente de 70 años, en posoperatorio de reemplazo total de cadera, quien presentó disnea súbita, dolor torácico leve y cursa con disminución de la saturación de oxígeno al examen físico, tenga embolismo pulmonar?

Según nuestro criterio clínico este paciente tiene una probabilidad de tener embolismo pulmonar del 85 %. Se ordenó una gammagrafía de perfusión pulmonar cuyo resultado se informó de “alta probabilidad” para embolismo pulmonar.

Entonces, para calcular la probabilidad postest debemos seguir los pasos indicados.

Primero. Convertir la probabilidad antes de la prueba o pretest, en razón antes de la prueba. Resolviendo según los datos del estudio, la razón pretest es igual a 0,85 / (1 – 0,85) = 0,85 / 0,15 = 5,6

Segundo. Obtener la razón postest, multiplicando la razón pretest por la razón de “alta probabilidad” para embolismo pulmonar. Resolviendo, es 5,6 por 18,4 = 103

Tercero. Convertir la razón postest en probabilidad postest, aplicando la formula, donde la probabilidad postest sería 103 / (1 + 103) × 100 = 99 %.

Es decir, la probabilidad que el paciente tenga un embolismo pulmonar, después de realizada la prueba pasó del 85 % al 99 %, lo cual confirma el diagnóstico de embolismo pulmonar.

Pero ¿qué hay si el resultado de la gammagrafía pulmonar en este paciente hubiera sido de “baja probabilidad”?

Primero. La razón pretest = 0,85 / (1 – 0,85) = 0,85 / 0,15 = 5,6

Segundo. La razón postest = 5,6 por 0,357 = 1,99

Tercero. Convertir la razón postest en probabilidad postest, así:

1,99 / (1 + 1,99) × 100 = 66,5 %.

En este caso, la probabilidad de tener la enfermedad sigue siendo muy alta (66,5 %), es decir, este paciente tiene una probabilidad de 33,5 % (que corresponde a 100 – 66,5 %) de tener un resultado falso negativo. Por esta razón, el clínico debe solicitar un angioTAC a este paciente, dado que esta última prueba es más sensible que la gammagrafía de perfusión pulmonar para embolismo pulmonar.

Ahora ¿Cuál es la probabilidad de que un paciente de 20 años, en posoperatorio de laparotomía por trauma cerrado de abdomen, quien presentó disnea progresiva, sin dolor torácico y cursa con disminución de la saturación de oxígeno al examen físico, tenga embolismo pulmonar?

Según nuestro criterio clínico este paciente tiene una probabilidad de tener embolismo pulmonar del 25 %. Se ordenó una gammagrafía de perfusión pulmonar cuyo resultado se informó como “normal”.

Entonces, para calcular la probabilidad postest debemos repetir los pasos descritos.

Primero. Convertir la probabilidad pretest, en razón pretest, que sería

Razón pretest = 0,25 / (1 – 0,25) = 0,25 / 0,75 = 0,33

Segundo. Obtener la razón postest, multiplicando la razón pretest por la razón de probabilidad de “normal”, o sea:

Razón postest = razón pretest de 0,33 por 0,1 = 0,033

Tercero. Convertir la razón postest en probabilidad postest, resolviendo la ecuación:

Probabilidad postest = 0,033 / (1 + 0,033) × 100 = 3,1 %.

Es decir, la probabilidad de tener un embolismo pulmonar, en este paciente de 20 años después de realizada la prueba, pasó del 25 % al 3,1 %, lo cual descarta el diagnóstico de embolismo pulmonar. En esta última situación no es necesario realizar angioTAC, pero se deben buscar otras entidades diferentes que puedan explicar el cuadro clínico.

Conclusión 

Las razones de probabilidad permiten resumir y complementar, en un solo valor, dos propiedades de las pruebas diagnósticas, sensibilidad y especificidad. Dado que su cálculo se hace a partir de esas propiedades, su valor es independiente de la prevalencia de la condición estudiada.

La gran utilidad de las razones de probabilidad es que permiten hacer explícito el cambio entre probabilidad pre y postest.

Las razones de probabilidad se pueden calcular cuando el resultado de la prueba de interés se expresa en forma dicotómica (positivo / negativo), en más de dos categorías o de forma ordinal.

Cumplimiento de normas éticas

Consentimiento informado: Este estudio es una revisión de la literatura, y como tal, no hay necesidad de un consentimiento informado ni de aprobación del Comité de Ética Institucional.

Conflicto de interés: Ninguno declarado por el autor.

Fuentes de financiación: Los recursos de financiación del proyecto provienen en su totalidad de aportes del autor.

Contribución del autor: El autor declara haber contribuido en la totalidad de la concepción y diseño del estudio, adquisición, análisis e interpretación de datos, redacción y revisión crítica del manuscrito.

Referencias – Razones de Probabilidad de la Enfermedad

1. Deeks JJ, Altman DG. Diagnostic tests 4: likelihood ratios. BMJ. 2004;329:168-9. https://doi.org/10.1136/bmj.329.7458.168

2. Halkin A, Reichman J, Schwaber M, Paltiel O, Brezis M. Likelihood ratios: getting diagnostic testing into perspective. QJM. 1998:91:247-58. https://doi.org/10.1093/qjmed/91.4.247

3. Silva Fuente-Alba C, Molina-Villagra M. Likelihood ratio (razón de verosimilitud): definición y aplicación en Radiología. Rev Argent Radiol. 2017;81:204-8. http://dx.doi.org/10.1016/j.rard.2016.11.002

4. Lang TA, Secic M. How to report statistics in medicine: annotated guidelines for authors, editors, and reviewers. Philadelphia: American College of Physicians, 1997.

5. Jaeschke R, Guyatt GH, Sackett DL, Bass E, Brill-Edwards P, Browman G, et al. Users’ guides to the medical literature: III. How to use an article about a diagnostic test B. What are the results and will they help me in caring for my patients? JAMA. 1994;271:703–7. https://doi.org/10.1001/jama.1994.03510330081039

Bibliografías – Razones de Probabilidad de la Enfermedad

6. Hayden SR, Brown MD. Likelihood ratio: a powerful tool for incorporating the results of a diagnostic test into clinical decision-making. Ann Emerg Med. 1999;33:575- 80. https://doi.org/10.1016/s0196-0644(99)70346-x

7. Guyatt GH, Oxman AD, Ali M, Willan A, McIlroy W, Patterson C. Laboratory diagnosis of iron-deficiency anemia: an overview. J Gen Intern Med. 1992;7:145-53. https://doi.org/10.1007/BF02598003

8. Akobeng AK. Understanding diagnostic tests 2: likelihood ratios, pre- and post-test probabilities and their use in clinical practice. Acta Paediatr. 2007;96:487-91. https://doi.org/10.1111/j.1651-2227.2006.00179.x

9. Fagan TJ. Letter: Nomogram for Bayes theorem. N Engl J Med. 1975;293:257. https://doi.org/10.1056/NEJM197507312930513

10. The PIOPED Investigators. Value of the ventilation/ perfusion scan in acute pulmonary embolism: results of the prospective investigation of pulmonary embolism diagnosis (PIOPED). JAMA. 1990;263:2753–9. https://doi.org/10.1001/jama.1990.03440200057023

Autor – Razones de Probabilidad de la Enfermedad

---

Eduardo de Jesús Torregroza-Diazgranados, Médico especialista en Cirugía general y subespecialista en Cirugía de Mama y Tejidos blandos;
Clínica de Cirugía de Mama, Bogotá, D.C., Colombia.

Fecha de recibido: 13/07/2020 – Fecha de aceptación: 30/09/2020 – Fecha de publicación en línea: 14/04/2021 Correspondencia: Eduardo de Jesús Torregroza-Diazgranados, Calle 111 No. 13-03, Bogotá, D.C., Colombia. Celular: 3175730414. Correo electrónico: torregrozad@gmail.com
Citar como: Torregroza-Diazgranados EJ. Pruebas diagnósticas: Razones de probabilidad. Rev Colomb Cir. 2021;36:403-10. https://doi.org/10.30944/20117582.717
Este es un artículo de acceso abierto bajo una Licencia Creative Commons – BY-NC-ND https://creativecommons.org/licenses/by-ncnd/4.0/deed.es