Caracterización de Péptidos de Alta Unión de la Proteina Ama-1 Mediante la Probabilidad y la Entropía

High Binding Peptides Characterization Of Ama-1 Protein Through Probability And Entropy

Javier Rodríguez1, Signed Prieto2, Pedro Bernal3, Catalina Correa4, Luisa Alvarez5,
Yolanda Soracipa6, Fredy López7, Sarith Vitery8

Resumen

La probabilidad y la entropía han sido empleadas para caracterizar física y matemáticamente péptidos de alta unión de proteínas de malaria al eritrocito. Estudios sugieren que la proteína AMA- 1 del Plasmodium Falciparum se une al eritrocito posiblemente jugando un papel en la infección. Se efectuó una cuantificación de la frecuencia de aparición de los 20 aminoácidos esenciales en cada una de las posiciones de los péptidos de 20 residuos que constituyen la proteína AMA-1, a partir de la construcción de un espacio de probabilidad no equiprobable, y se calcularon los valores de probabilidad, sumatoria de probabilidad y entropía para cada una de las secuencias peptídicas.

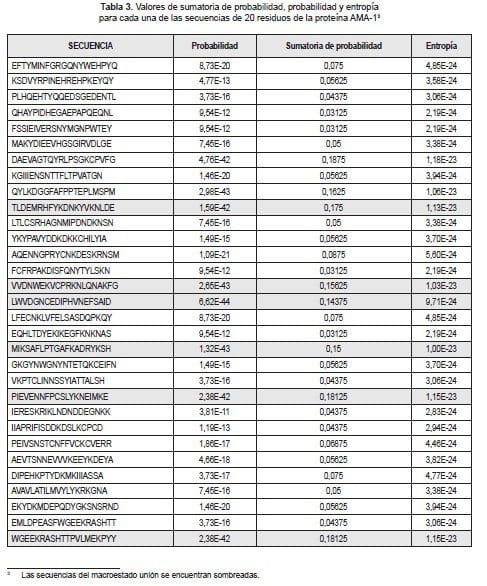
Se encontró que los valores de probabilidad, sumatoria de probabilidad y entropía para las secuencias que no se unen varían entre los valores asociados al macroestado de no unión, mientras que dichos valores para las secuencias específicas de unión comprobadas experimentalmente se encuentran fuera de dichos rangos, conformando rangos específicos diferenciados asociados al macroestado de unión.

Se diferenciaron secuencias de unión y de no unión con la metodología empleada, acertando en el 100% de los casos estudiados, caracterizando así los péptidos de AMA-1 de una forma objetiva y reproducible, y evidenciando un orden físicomatemático subyacente al fenómeno de unión.

Palabras clave: AMA-1, Probabilidad, Entropía, Unión, Eritrocito.

Abstract

Probability and Entropy have been used to physically and mathematically characterize high binding peptides of Malaria proteins to the erythrocyte. Studies suggest that AMA-1 protein of Plasmodium Falciparum binds to erythrocyte, possibly playing a role in the infection.

It was made a quantification of the frequency of appearance of the 20 essential amino acids in each one of the positions in peptides about 20 residues that form the AMA-1 protein, beginning with the building of a non equiprobable space of probability, and values of probability, probability summation and entropy were calculated for each of the peptide’s sequences.

It was found that probability, probability summation and entropy values for the not-binding sequences vary between the values associated to the not-binding macrostate, while those values for the specific experimentally binding sequences are out of that ranges, conforming specific differentiated ranges associated to the binding macrostate.

Binding and not-binding sequences were differentiated with the used methodology, with a 100% success for the studied cases, characterizing the AMA-1 peptides in an objective and reproducible way, and showing a physical-mathematical subjacent order to the binding phenomenon.

Key words: AMA-1, Probability, Entropy, Binding, erythrocyte.

Introducción

La probabilidad es una medida adimensional usada para cuantificar la posibilidad de ocurrencia de un resultado particular dentro de un número limitado de eventos, el cual se denomina espacio muestral (Laplace, 1995; Feynman et al, 1964a; Mood et al, 1974; Blanco, 1996).

La termodinámica y la mecánica estadística son las respuestas teóricas a la dificultad de determinar la dinámica de los eventos en los sistemas compuestos por un gran número de moléculas, un examen que sería imposible a partir del estudio individual de las partículas, como en el caso de un gas, porque sería necesario integrar una ecuación diferencial para cada uno de los componentes (Tolman, 1979; Matvéev, 1987; Feynman et al, 1964b). La entropía fue definida inicialmente por Boltzmann como una medida proporcional al logaritmo del número de microestados que posee un sistema en estado de equilibrio y que permanece invariable desde el punto de vista macroscópico (Feynman et al, 1964b).

Esta definición fue aplicada originalmente en el contexto de la teoría cinética de los gases y luego con la llegada de la mecánica estadística se extendió a los sistemas fuera de equilibrio, partiendo de las probabilidades de las distribuciones microscópicas como una medida proporcional a la suma de los productos de la probabilidad de cada microestado por su logaritmo, dada una constante de proporcionalidad, la constante de Boltzmann (Feynman et al, 1964b). Esta misma concepción fue usada por Claude E. Shannon en el contexto de la teoría de la información para cuantificar objetivamente la cantidad de información que posee el sistema, o sea la información contenida en un mensaje (Frodden et al, 2004).

La malaria o paludismo es una de las enfermedades tropicales de mayor relevancia, presentándose un estimado de 248 millones de casos y 863.000 muertes en el año 2008 a nivel mundial, cifras similares a las del 2006. Esta enfermedad afecta principalmente a países en vía de desarrollo, donde adquiere dimensiones epidémicas (WHO, 2009). Para la región de las Américas, de acuerdo con la OMS, aproximadamente el 32% de los individuos es infectado por Plasmodium falciparum. Durante el ciclo eritrocítico de la enfermedad se da una invasión periódica mediante el reconocimiento, unión, orientación e internalización del parásito en las células rojas; dicho fenómeno depende de la interacción ligando receptor de alta especificidad entre los antígenos de superficie del parásito y moléculas en la membrana eritrocítica (WHO, 2009; Aikawa et al, 1978; Hadley, 1986).

1 MD. Director Grupo Insight – Cínica del Country. Docente Línea de Profundización e Internado Especial Física y Matemáticas aplicadas a la Medicina – Universidad Militar Nueva Granada.
2 Investigadora Grupo Insight. Clínica del Country.
3 Investigadora Grupo Insight. Clínica del Country.
4 PSY. Investigadora Grupo Insight. Clínica del Country. Docente Línea de Profundización e Internado Especial: Física y Matemáticas aplicadas a la Medicina – Universidad Militar Nueva Granada.
5 PSY. Investigadora Grupo Insight.
6 Investigadora Grupo Insight. Clínica del Country. 7 Investigador Grupo Insight – Clínica del Country.
7 Estudiante Medicina. Internado Especial: Física y Matemáticas Aplicadas a Medicina. Universidad Militar Nueva Granada
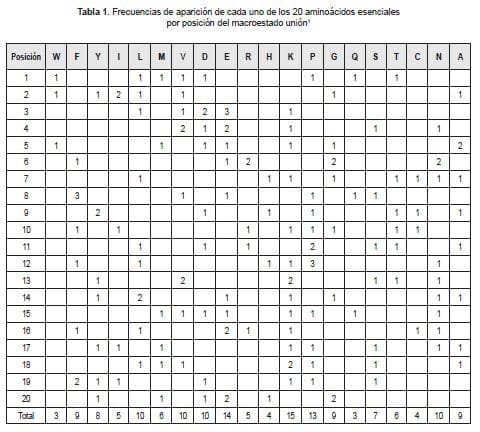
8 Los espacios en blanco corresponden a frecuencias de aparición equivalentes a cero.
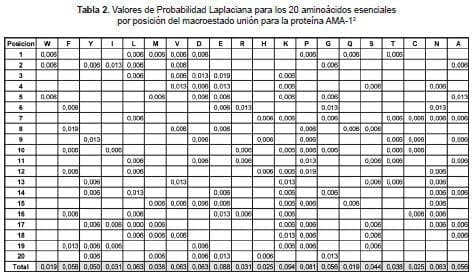
9 Los espacios en blanco corresponden a valores de probabilidad iguales a cero

La proteína AMA-1 del Plasmodium Falciparum es sintetizada en los esquizontes segmentados maduros (Hodder et al, 1996; Waters et al, 1990), su peso molecular es de 83kDa (Hodder et al, 1996); está asociada al complejo apical y se localiza en la superficie del merozoito durante la ruptura del esquizonte (Narum, 1994). La función biológica de la proteína AMA-1 es desconocida; sin embargo, estudios sugieren que se trata de una proteína de unión al eritrocito, así como existe evidencia experimental de su posible papel protectivo contra la infección de algunos tipos de Plasmodium en la inmunización en ratones (Collins et al, 1994; Anders et al, 1998; Thomas et al, 1984).

Rodríguez desarrolló una metodología de caracterización de péptidos de alta unión al eritrocito, en donde mediante la aplicación de la teoría de la probabilidad y la entropía a la proteína de superficie del merozoíto MSP-1, se encontró que los valores de sumatoria de probabilidad, probabilidad y entropía para las secuencias específicas comprobadas experimentalmente de alta unión varían entre los rangos asociados al macroestado unión, mientras que fuera de estos rangos se encuentran todos los valores de los péptidos encontrados experimentalmente de no unión (Rodríguez, 2008a), realizando una diferenciación con un acierto del 100% en los casos estudiados; esta metodología fue aplicada posteriormente a la caracterización física y matemática de las secuencias de alta unión de las proteínas EBA-140 y MSA-2 (Rodríguez et al, 2009a; Rodríguez et al 2009b), logrando el mismo grado de acierto en la diferenciación.

La proteína AMA-1 está conformada por 31 secuencias de 20 aminoácidos, de las cuales 8 han sido comprobadas experimentalmente de alta unión (Urquiza et al, 2001). El propósito de este trabajo es realizar una caracterización física y matemática de la unión de péptidos de AMA-1 al glóbulo rojo, mediante la aplicación de la teoría de la probabilidad y la ley de la entropía.

Definiciones

Macroestado: fueron definidos dos macroestados, donde el macroestado de unión se asocia a las secuencias que presentan alta unión y el macroestado de no unión corresponde a las secuencias que no presentan alta unión (Rodríguez, 2008a).

Microestado: Toda secuencia específica de veinte aminoácidos (Rodríguez, 2008a).

Probabilidad Laplaciana: La probabilidad de un aminoácido A en una posición específica i es definida como la división de la frecuencia de aparición de tal aminoácido en dicha posición entre el total de aminoácidos (Laplace, 1995; Feynman et al, 1964a; Mood et al, 1974; Blanco, 1996).

Sumatoria de probabilidad:  Para una secuencia específica, corresponde a la sumatoria de la probabilidad de aminoácidos componentes, siendo la cuantificación matemática de las probabilidades de aparición de cada aminoácido por posición (Rodríguez, 2008a).

Probabilidad de una Secuencia: se define como  la multiplicación de las probabilidades asociadas a los aminoácidos que la componen por posición específica i (Laplace, 1995; Feynman et al, 1964a; Mood et al, 1974; Blanco, 1996).  Entropía: En un sistema cuyos microestados no son equiprobables la entropía de un péptido está dada por: Donde k es igual a la constante de Boltzmann, 1.38×10-23 (J/k), S el valor de la entropía (Tolman, 1979; Matvéev, 1987) y P (Ai) es el valor de la probabilidad del aminoácido A en la posición i.

Metodología

Esta metodología está basada en un trabajo previo en el que se realizó una caracterización de los péptidos de alta unión de la proteína de superficie MSP-1 por medio de la aplicación de la probabilidad y la entropía (Rodríguez, 2008a).

A partir de las 31 secuencias no sobrelapadas de 20 aminoácidos de la proteína AMA-1, se construyó un espacio de probabilidad con el que se cuantificó la frecuencia de aparición de cada uno de los 20 aminoácidos esenciales en cada una de las 20 posiciones posibles para los 8 péptidos comprobados experimentalmente de alta unión y luego se empleó el cálculo de la probabilidad Laplaciana (Ecuación 1) para evaluar la probabilidad de cada uno de los 20 aminoácidos esenciales en cada posición para todas las secuencias estudiadas.

La proteína completa es escogida a fin de caracterizar matemáticamente los dos macroestados (ver definiciones) y construir un espacio de probabilidad no equiprobable que cuantifique las secuencias de alta unión. Partiendo del espacio de probabilidad construido, se efectúan los cálculos de sumatoria de probabilidad (Ecuación 2), probabilidad (Ecuación 3) y Entropía (Ecuación 4), para cada una de las 31 secuencias de la proteína AMA-1.

3 Las secuencias del macroestado unión se encuentran sombreadas.