La Teoría de las Derivaciones Unipolares de Wilson

En el párrafo 13, página 282 del artículo Sobre el Triángulo de Einthoven, la teoría de derivaciones Electrocardiográficas unipolares y la interpretación del electrocardiograma precordial Wilson y colaboradores escribieron:

“Se ha demostrado que la suma de las diferencias de potencial entre cualquier número de electrodos y un punto común conectado a estos electrodos a través de resistencias iguales debe de ser cero como consecuencia de la primera Ley de Kirchhoff. El potencial del terminal central es consecuentemente igual en cada instante al promedio de los potenciales de los electrodos de las extremidades”.

En el primer párrafo, los autores demuestran un concepto errado de las leyes de Kirchhoff. Estas leyes, vigentes desde 1845 sin modificaciones, son:

Primera Ley, también llamada teorema de las uniones dice:

La suma de las corrientes que salen y la suma de las corrientes que llegan a una unión dentro de un circuito eléctrico son iguales a cero. Su expresión matemática es:

∑n In = 0 (11)

La primera Ley de Kirchhoff se aplica al flujo de la corriente y nó al voltaje de la corriente. Esta ley no nos permite deducir que el voltaje de la unión de las tres resistencias sea igual a cero, como lo describe Wilson. (Lea también: Validez de la Teoría del Triángulo Equilátero)

Segunda Ley, o la ecuación de circuitos cerrados dice:

En cada circuito cerrado, la suma de las fuerzas electromotrices es igual a la suma de las caídas de potencial. Su expresión matemática es:

Vg = R1 I1 + R2 I2 + R3 I3 +…….Rn In (12)

La segunda Ley de Kirchhoff demuestra todo lo contrario de la conclusión de Wilson. Según esta ley, si Vg tiene un valor diferente a cero, los potenciales eléctricos de las uniones, dentro del circuito, son diferentes a cero. Estos solo pueden ser iguales a cero cuando el valor de Vg es igual a cero.

Esta ley es la que nos muestra que si conectamos tres cables a tres tomacorrientes dentro del hogar y conectamos al alambre vivo de cada uno de los cables a una resistencia de 50.000Ω y unimos el extremo libre de las tres resistencias para formar un punto común, como lo sugiere Wilson, no es una buena idea tocar el punto común y el alambre conectado a tierra.

Es más, si no se está bien aislado podría ser fatal solo tocar el punto común. El voltaje del punto común depende del voltaje generado y de las caídas de potencial a través de las resistencias presentes en el circuito eléctrico. En este ejemplo el voltaje inicial es 110 voltios, la caída de potencial a través de las resistencias de 50.000Ω no nos protege de un buen choque eléctrico.

La aseveración de Wilson en el segundo párrafo nunca ha sido estudiada o demostrada. El flujo de la corriente eléctrica dentro del circuito eléctrico de las derivaciones unipolares varia constantemente, alterando la construcción del punto común según el ángulo del dipolo como se verá en los siguientes diagramas.

En el mismo párrafo 13, de la página 282 del mismo artículo, Wilson continúa:

”Sobre las bases de las asunciones en las cuales se apoya el Triángulo equilátero de Einthoven, Fahr y de Waart, más la asunción de que las fuerzas eléctricas de origen cardiaco que son perpendiculares al plano de las derivaciones estándar de las extremidades no tienen un efecto significativo sobre las variaciones de potencial de las extremidades, se ha demostrado que el potencial del terminal central conectado a través de resistencias iguales a electrodos colocados en el brazo derecho, el brazo izquierdo, y la pierna izquierda no está afectado materialmente por la contracción del corazón y se puede considerar constante durante todo el ciclo cardíaco”.

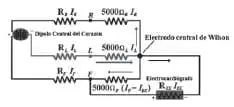
Esquema del circuito eléctrico de la derivación V1 de Wilson en el instante en que el dipolo está a un ángulo de 150 grados.

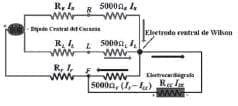
Esquema del circuito eléctrico de la derivación V1 de Wilson en el instante en que el dipolo está a un ángulo de 90 grados.

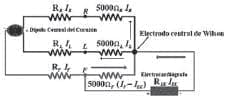
Esquema del circuito eléctrico de la derivación V1 de Wilson en el instante en que el dipolo está a un ángulo de -90 grados.

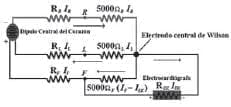
Esquema del circuito eléctrico de la derivación V1 de Wilson en el instante en que el dipolo está a un ángulo de 30 grados.

Perpendiculares al plano de las derivaciones estándar de las extremidades no tienen un efecto significativo sobre las variaciones de potencial de las extremidades, se ha demostrado que el potencial del terminal central conectado a través de resistencias iguales a electrodos colocados en el brazo derecho, el brazo izquierdo, y la pierna izquierda no está afectado materialmente por la contracción del corazón y se puede considerar constante durante todo el ciclo cardíaco”.

En este párrafo Wilson nuevamente ignora la realidad. Con los estudios de Smith, Wood, Baylis y muchos otros investigadores, para el año de 1946, ya eran bien conocidos los cambios producidos durante los infartos agudos de la pared anterior y la pared posterior en las tres derivaciones estándar de Einthoven.

Estos cambios demuestran que la asunción de Wilson es errada. Irónicamente, los vectores de los infartos de la pared lateral del ventrículo izquierdo, que según las teorías, estarían en el plano del Triángulo Equilátero de Einthoven brillan por su ausencia.

Las derivaciones unipolares de Wilson no llenan tres de las premisas que ellos mismos propusieron. Primero, la primera ley de Kirchhoff no demuestra que el potencial de la unión de las tres resistencias sea cero, segundo, el triángulo de Einthoven no existe y tercero, los potenciales generados por el corazón, perpendiculares al triángulo, sí afectan a las tres extremidades.