Interpretación Clínica: De los Experimentos Clínicos en Cáncer

EDUARDO TORREGROZA-DIAZGRANADOS, MD*

Palabras clave: ensayos clínicos controlados, investigación clínica, epidemiología.

Resumen

La evaluación del beneficio de una terapia es crucial para decidir si un nuevo tratamiento debe ser usado.

Los clínicos que utilizan los resultados de los experimentos clínicos para guiar su práctica médica necesitan herramientas útiles para evaluar la importancia clínica de los resultados estadísticamente significativos antes de introducir una nueva terapia en cáncer en la práctica clínica.

El objetivo de esta revisión es proponer a los intervalos de confianza como los instrumentos útiles para juzgar la importancia clínica de un tratamiento, dado que éstas hacen explícita la evaluación del beneficio de una terapia y permiten atenuar el énfasis de la interpretación de los experimentos clínicos sólo con base en el criterio estadístico.

Introducción

El experimento clínico (EC) es el instrumento metodológico más sólido para evaluar la efectividad de nuevos tratamientos contra el cáncer. Dado el papel fundamental del EC en la evaluación de una terapia, éste se ha convertido en un elemento decisivo para la toma de decisión en la recomendación de una nueva terapia.

En las revistas biomédicas cada año se publican un número importante de EC, cuyos resultados muestran que una nueva terapia es superior a la usual.

Por lo regular, un valor de p menor a 0,05 se toma como criterio para establecer que el nuevo tratamiento es superior al aceptado en ese momento, y con base en este criterio estadístico se considera que el resultado del ensayo clínico es estadísticamente significativo.

Sin embargo, los resultados del EC deben evaluarse con el propósito de establecer cuál debería ser el mejor tratamiento para los pacientes, y también para saber si el beneficio de la nueva terapia es tan importante clínicamente que ésta debería ser introducida en la práctica médica habitual.

Desde esta última perspectiva, se deben tener en cuenta la magnitud y la importancia clínica del efecto terapéutico del tratamiento y no sólo la significación estadística (1). Muchos reportes de ensayos clínicos no proveen información respecto a la importancia clínica de sus resultados.

Moher y cols. encontraron que de 120 EC con resultados estadísticamente significativos, sólo 20% de ellos tenían cualquier comentario sobre su importancia clínica (2). Chan y cols., en un estudio más reciente, encontraron que los resultados de los experimentos clínicos se interpretaron desde la perspectiva de la importancia clínica en 20 de 27 EC evaluados (74%);. de estos 20, en cinco de ellos (25%) hubo justificación para la interpretación clínica de los resultados (3).

La evaluación del beneficio de una terapia, que concierne a la valoración de la importancia clínica de un efecto terapéutico, es muy difícil. Justamente, el objetivo de esta revisión es poner a consideración los intervalos de confianza (IC) para evaluar la importancia clínica del efecto terapéutico de un tratamiento.

En esta revisión se discuten los conceptos de las medidas de significación estadística comúnmente reportados en los ensayos clínicos de cáncer, se propone la definición de significación clínica y, por último, se exponen los IC como medida de significación clínica.

Evaluación de la Validez y la Significación Estadística de los Resultados del Experimento Clínico

Un resultado estadísticamente significativo puede deberse a tres factores:

1. Sesgo.
2. Azar.
3. Efecto terapéutico del tratamiento.

La comparación de dos tratamientos sería sencilla si pudiéramos incluir en el EC a la totalidad de las personas con la condición bajo estudio. Sin embargo, tal situación es imposible de lograr por las exigencias logísticas y financieras que esto implicaría. A cambio de ello, evaluamos los tratamientos bajo estudio sólo en una proporción o muestra de personas de todas las posibles. No obstante, para hacer posible la evaluación de un tratamiento en el mundo real irremediablemente debemos asumir los riegos de ciertos errores.

En la interpretación de un EC es muy importante considerar la presencia de sesgos en el estudio, por lo cual se hablará primero de este tipo de error.

Un EC se puede considerar como un instrumento de medición; el objetivo es evaluar o medir objetivamente los resultados o desenlaces en cada grupo de tratamiento, de tal forma que cualquier diferencia encontrada en los grupos sea reflejo de las diferencias de efectividad entre los tratamientos evaluados.

Como ejemplo: un EC encontró que el tratamiento A es mejor que el B. Además, los pacientes asignados a la terapia B, deliberadamente, no cumplieron con el tratamiento decidido en el estudio debido a reacciones inesperadas de efectos secundarios de esta terapia. Este factor, falta de adherencia al tratamiento, es el responsable en sí de los resultados de este EC; mas no se puede afirmar que los resultados son debidos a la menor eficacia de la terapia B.

Se le denomina sesgo a cualquier factor o proceso que tienda a producir resultados sistemáticamente diferentes a los verdaderos (4).

La asignación aleatoria del tratamiento, cegamiento, seguimiento adecuado y análisis pragmático de los datos evitan la introducción de sesgos en el EC, lo cual asegura un resultado válido de la comparación de los tratamientos (5).

De otro lado, una de las funciones de la estadística en el análisis de los datos de un EC es el de servir como herramienta para diferenciar entre los resultados que pudieran ser debidos al azar de aquellos como consecuencia del efecto terapéutico del tratamiento.

La prueba de hipótesis y los IC son los procedimientos o medidas estadísticas más utilizados en los EC como criterio diferenciador entre estos dos tipos de resultados.

A) Prueba de significación estadística y prueba de hipótesis de Neyman-Pearson

Hasta 1970 el concepto estadístico que prevalecía era el de establecer si el azar podría ser el responsable de un resultado particular en un estudio. Los únicos métodos para evaluar esta proposición eran la prueba de significación estadística y la de hipótesis de Neyman-Pearson. Ante la similitud de estos métodos, el término “prueba de significación estadística” se aplica a ambos. Sin embargo, las pruebas de significación estadística y la prueba de hipótesis de Neyman-Pearson son corrientes de pensamiento bien diferentes (6). Dada la importancia de estas dos escuelas en el desarrollo de la inferencia estadística, se comentarán los aspectos más relevantes de cada uno de ellos.

Prueba de significación estadística

La idea de significación estadística fue introducida por R A Fisher. En el enfoque de Fisher se especifica una hipótesis nula, la cual es una hipótesis de no asociación entre dos variables. Para el caso de un EC en el que se comparan dos tratamientos, como hipótesis nula se establece que no existen diferencias entre los tratamientos evaluados.

El valor de P es el criterio utilizado para evaluar la hipótesis nula en la prueba de significación estadística; además, es la probabilidad, bajo el supuesto que la hipótesis nula es correcta, de encontrar un resultado igual o más extremo que el observado en el estudio y el supuesto que no hay fuentes de sesgo en la recolección de los datos o en el proceso de análisis.

En la prueba de significación estadística valores de P muy pequeños indican bajo grado de compatibilidad entre la hipótesis nula y los datos del estudio.

Esta incompatibilidad se deriva del hecho de que un valor de P muy pequeño representa baja probabilidad de que un estadístico de prueba tan extremo o más extremo que el estadístico observado pudiera ser generado si la hipótesis nula fuera verdad (6).
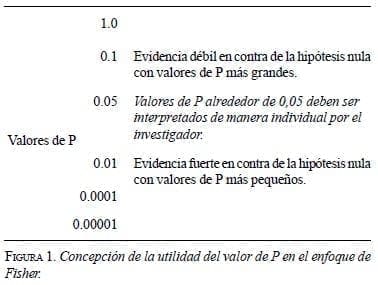
En el enfoque de significación estadística el valor de P es un índice que mide la fuerza de evidencia contra la hipótesis nula. Así,Fisher propuso que valores de P menores a 0,05 fueran tomados como criterios de evidencia en contra de la hipótesis nula, pero no como criterio absoluto. Por ejemplo, un valor de P alrededor de 0,05 no podría llevar ni al rechazo ni a la aceptación de la hipótesis nula, sino a la decisión de realizar otro experimento.

La concepción del valor de P en el proceso de significación estadística se ilustra en la figura 1.

Prueba de hipótesis de Neyman-Pearson

En el enfoque de Neyman-Pearson se establecen unas reglas de decisión para interpretar los resultados del estudio con antelación a la realización de éste, y el resultado del análisis es sencillamente el rechazo o la aceptación de la hipótesis nula. La primera de ellas fija un punto de corte, usualmente 0,05 ó 0,01, para juzgar al valor de P y este criterio se usa para rechazar o no a la hipótesis nula (si P es menor o igual a 0,05 se rechaza la hipótesis nula, si P es mayor a 0,05 se acepta).

Este punto de corte escogido por el investigador en el diseño del estudio se denomina nivel alfa y es uno de los aspectos más distintivos del enfoque de Neyman-Pearson (6).

En contraste con el enfoque de Fisher, bajo la perspectiva de Neyman-Pearson los valores de P no son interpretados, sino que el valor P es evaluado con respecto al nivel alfa preestablecido.

Hay que tener en cuenta siempre la diferencia entre el nivel alfa y el valor P en esta escuela. El nivel alfa se especifica en el diseño y planeación del estudio y el valor de P es la cantidad derivada del estudio una vez concluidos y analizados los datos de éste.

En segundo lugar, en el enfoque de NeymanPearson se debe especificar una hipótesis alterna lo más precisa posible. Es decir, no basta con sólo señalar que no hay diferencias entre los tratamientos evaluados, sino que hay que indicar cuánto es mejor el tratamiento para evaluar que el de comparación (7).

En tercer lugar, Neyman y Pearson argumentaron que había dos tipos de errores que se podrían cometer al interpretar los resultados de un estudio (tabla 1) (7).

Si la hipótesis para probar es realmente verdadera y ésta se rechaza de manera errónea a favor de la alterna, se comete un error tipo I. Si la hipótesis para probar es realmente falsa y ésta no se rechaza, se comete un error tipo II.

El riesgo de cometer el error tipo II se designa con una probabilidad: probabilidad beta. El complemento del error beta es el poder de un estudio, el cual se puede definir como la probabilidad que tiene un estudio para detectar diferencias entre tratamientos cuando realmente existen (7). En otras palabras, el poder de un estudio es la probabilidad de evitar el error tipo II.

Por último, se reafirma que un valor de p nunca puede probar la verdad de una hipótesis.

El legado del pensamiento de Fisher y Neyman-Pearson ha sido muy influyente y constituye la base para el diseño de todo el andamiaje de un EC en el día de hoy.

En el diseño de todo EC se formulan dos tipos de hipótesis acerca del beneficio de la nueva terapia: hipótesis nula e hipótesis alterna. La primera afirma que no hay diferencias entre los tratamientos evaluados; la segunda, que hay diferencias entre los tratamientos evaluados.

La hipótesis alterna puede ser bilateral, a dos colas, cuando no se indica la dirección del efecto terapéutico: el nuevo tratamiento evaluado puede ser mejor o peor que el habitual; o unilateral, a una cola, cuando se indica la dirección del efecto terapéutico: el nuevo tratamiento es mejor que el usual; el nuevo tratamiento es peor que el usual.

La hipótesis alterna a dos colas es la más utilizada, dado que no prejuzga la dirección de la efectividad efectividad de un tratamiento. El planteamiento de la hipótesis alterna define si la prueba de significancia estadística es empleada a una o dos colas.

En el diseño del EC también se define el nivel alfa (usualmente 0,05) y un poder adecuado para detectar diferencias clínicamente importantes, si las hubiera (80 a 90% de poder).

En ocasiones, son difíciles de entender los conceptos de error alfa, error tipo I, error tipo II, poder del estudio. Una manera fácil de asimilar los conceptos antes expuestos consiste en relacionar los resultados y conclusiones de un experimento clínico con el análisis de una prueba diagnóstica (8) (tabla 2).

Los clínicos utilizan las pruebas diagnósticas con el propósito de establecer la presencia o ausencia de la condición estudiada. En investigación clínica, con base en los datos evidenciados en el EC, se trata de establecer la verdadera relación entre dos o más terapias.

Las filas en la tabla 2 corresponden a los resultados de la prueba diagnóstica y las conclusiones derivadas de los resultados del EC; las columnas, a la condición verdadera del individuo y la relación real entre los tratamientos.

Cuando los resultados de un EC evidencian que un tratamiento es superior a otro y en verdad esta relación es cierta, se llega a la conclusión correcta (verdaderos positivos, celda a).

Cuando se concluye que no hay diferencia entre los tratamientos y en verdad esta relación es cierta, se llega nuevamente a la conclusión correcta (verdaderos negativos, celda d).

Lo que se espera evitar son las conclusiones falsas de las celdas b y c. Cuando se concluye que existe una diferencia entre los tratamientos comparados y en verdad no hay diferencia entre ellos, se comete un error tipo I (falsos positivos, celda b).

Cuando se concluye que no hay diferencias en los tratamientos evaluados y realmente sí existe di diferencia entre ellos, se comete un error tipo II (falsos negativos, celda c).

El poder del estudio es análogo a la sensibilidad de una prueba diagnóstica. La tabla 3 resume los principales errores en la interpretación de P.

B) Intervalos de confianza

Como en el EC se ha estudiado sólo una muestra de individuos y dado que existe variabilidad inherente entre cada sujeto estudiado, la verdadera magnitud del efecto terapéutico será mucho más grande o más pequeña que la calculada por el EC.

Sin embargo, se puede calcular un rango de valores alrededor del valor puntual estimado, que con una alta probabilidad (usualmente de 95%) contenga el verdadero valor de la magnitud del efecto. Este intervalo de valores se conoce con el nombre de IC.

Una definición e interpretación útil del IC se basa en el concepto de frecuencia. Un IC determinado (95%) significa que si se toman 100 muestras de un mismo tamaño y se utiliza cada muestra para construir un IC del 95%, se podría esperar que en promedio 95 de los intervalos cubrieran el verdadero efecto de la terapia y cinco no lo hicieran (9).

Existe una relación entre el IC y la prueba de hipótesis: cuando el intervalo del 95% no contiene el cero (0) hay una diferencia estadísticamente significante (p<0,05), mientras que si el IC contiene el 0 no hay una diferencia estadísticamente significante (p>0,05).

El IC puede utilizarse como medida de significación estadística o, mejor aún, como medida de significación clínica.

---

* Cirujano de Seno y Tejidos Blandos. Cansercoop (Precooperativa de Servicios Médicos Asociados en Cáncer). Bogotá, Colombia.

Evaluación de la Significación Clínica

La significación clínica se puede definir como el efecto terapéutico más pequeño de una terapia que podría impactar en el manejo clínico de los pacientes, dado sus efectos secundarios, costos e inconvenientes (10).

Una vez se ha determinado que el EC muestra una diferencia entre los tratamientos evaluados, el siguiente paso es calcular la magnitud de la diferencia observada en el EC.

La magnitud del efecto de una nueva terapia se calcula mediante tres medidas de efecto y se consideran consideran medidas de estimación puntual de efecto: reducción absoluta del riesgo (RAR), número necesario para tratar (NNT), reducción relativa del riesgo (RRR) (11).

Con el propósito de ilustrar los cálculos para cada una de estas medidas se revisa el Intergrup Exemestane Study (IES), el tercer EC reportado como terapia adyuvante en cáncer de seno, usando inhibidores de aromatasa (12). El IES es un experimento clínico que asignó a mujeres con cáncer primario de seno que habían recibido dos a tres años de tratamiento adyuvante con tamoxifeno a dos esquemas de terapias: seguir su tratamiento con tamoxifeno durante cinco años, o cambiar (después de dos a tres años de tamoxifeno) a terapia secuencial con exemestane.

Este estudio fue diseñado con un poder de 88% para detectar una diferencia absoluta en supervivencia libre de enfermedad de 3,6% a tres años de seguimiento.

A 36 meses de seguimiento la supervivencia libre de enfermedad fue 86,8% en el grupo de mujeres que siguieron con tamoxifeno y 91,5% en el grupo que cambió a exemestane después de dos a tres años de tamoxifeno.

Estos resultados también pueden expresarse en su complemento, es decir, el riesgo de recurrencia: el riesgo de recurrencia a tres años fue 13,2% para tamoxifeno frente a 8,5% para exemestane. La reducción absoluta del riesgo se consigue mediante la diferencia de los resultados de eventos adversos entre los grupos comparados. En el ejemplo anterior, la RAR fue del 4,7%: 13,2 – 8,5% = 4,7%. Este porcentaje significa que el exemestane rescató a 4,7% de las pacientes destinadas a presentar recidiva.

Los resultados de la RAR se pueden presentar de otra forma. Un RAR de 4,7% también señala que por cada 100 pacientes el exemestane evitó la recurrencia en 4,7 pacientes. ¿Cuántos pacientes son necesarios para evitar sólo una recurrencia? La respuesta se obtiene con una regla de tres simple: Por cada 100 pacientes 4,7 pacientes sin recurrencia.

¿Cuántos pacientes son necesarios (X) para evitar sólo 1 recurrencia?

Al despejar X tenemos: 100 por 1 dividido por 4,7= aproximadamente 22 pacientes.

Se requieren 22 pacientes para evitar una recurrencia. Este resultado es el número necesario para tratar. Es decir, que el número necesario para tratar es el inverso de la reducción absoluta del riesgo.

La reducción del riesgo relativo es la disminución de eventos adversos alcanzada por el trata tratamiento, expresada como una proporción del grupo control. Así, la reducción del riesgo relativo es la diferencia en los porcentajes de eventos entre el grupo control y el experimental, dividido por el porcentaje de eventos del grupo control: (% eventos adversos en el grupo control -% eventos adversos en el grupo experimental) /% eventos adversos en el grupo control, por 100.

En el ejemplo, [(13,2% menos 8,5%) entre 13,5] por 100 = 35,6%; esta es la reducción relativa del riesgo.

La tabla 4 resume las fórmulas para el cálculo de las medidas puntuales de efecto.

El intervalo de confianza es la medida de significación clínica más importante para la mejor interpretación de un ensayo clínico.

Intervalos de confianza

Los IC no deben utilizarse con el único propósito de examinar la significancia estadística al nivel convencional del 5%, sino más bien para evaluar la importancia clínica de los resultados estadísticamente significativos.

Cuando un EC encuentra una diferencia significativa, el IC facilita la distinción entre una diferencia estadísticamente significante de una clínicamente importante. Para hacer esto posible, es necesario establecer establecer la magnitud del efecto terapéutico que pueda considerarse como un efecto terapéutico clínicamente importante (ECI) y expresarlo en una medida de efecto puntual (de preferencia RAR).

Pero, ¿cómo se puede deducir el valor del ECI?

La determinación del ECI se puede establecer siguiendo dos enfoques:

1. A partir de la diferencia mínima considerada para el cálculo del tamaño de la muestra del EC para detectar entre los tratamientos evaluados.

2. Teniendo en cuenta los riesgos de la terapia, costos y el desenlace evaluado en el EC.

La diferencia mínima para detectar entre los tratamientos es utilizada por los investigadores para el cálculo del tamaño de la muestra y se describe es la sección de materiales y métodos del EC.

Este valor se propone como el ECI de base, ya que es el establecido por los propios investigadores que diseñaron y realizaron el EC.

Se puede ser riguroso con el valor del ECI cuando los riesgos de la terapia sean grandes, produzca efectos secundarios graves y cuando la terapia sea costosa, o se puede ser flexible, cuando el desenlace evaluado es poco relevante para el paciente, la terapia no tiene riesgos ni efectos secundarios graves.

Para ilustrar los cálculos de la utilidad de los IC como medida de significación clínica se utilizan como ejemplo los resultados reportados por los estudios MA17 y ATAC.

El tamoxifeno es el tratamiento adyuvante establecido para mujeres posmenopáusicas con cáncer temprano de seno y receptores positivos. Cinco años de tratamiento se ha establecido como la duración óptima de este medicamento como terapia adyuvante en pacientes con cáncer primario de seno.

El MA17 es un EC para evaluar el papel de la terapia endocrina extendida más allá de cinco años, comparando letrozol contra placebo en mujeres que habían completado cinco años con tamoxifeno y estaban libres de recurrencia (13). El resultado primario para evaluar en el estudio fue la supervivencia libre de enfermedad.

Este estudio se diseñó con un poder de 80% para detectar una diferencia de 2,5% en supervivencia libre de enfermedad a cuatro años de seguimiento.

Luego de este período la supervivencia libre de enfermedad fue de 93% para pacientes tratadas con letrozol y de 87% para el grupo que recibió placebo.

Con los datos reportados en el MA17 se establece que el ECI fue alrededor del 2,5%. En segundo lugar, debe calcularse la magnitud del efecto terapéutico en el ensayo clínico mediante una medida puntual de efecto (RAR) y finalmente calcular los intervalos de confianza para la RAR observada en el EC, con base en las fórmulas suministradas en la tabla 5.

La reducción absoluta del riesgo en el MA17 fue de 6%: 13 – 7%= 6%. Luego, se calcula el intervalo de confianza del RAR: límite inferior del intervalo de confianza de 4,3; límite superior del intervalo de confianza 7,6; (RAR 6, IC 4,3 a 7,6). Con estas medidas en mente se puede valorar la importancia clínica del resultado estadísticamente significativo detectado en el EC.

Un efecto terapéutico puede considerarse estadísticamente significativo y clínicamente importante en dos circunstancias: la primera, cuando un EC encuentra un efecto terapéutico muy importante y éste es de tal magnitud que el valor del límite inferior del IC de la RAR es mayor que el efecto clínicamente importante (figura 2, EC IA).

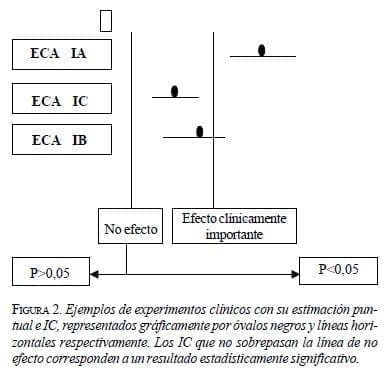
La segunda, cuando un EC encuentra un efecto terapéutico (RAR) mayor que el ECI, pero no tan grande como en la circunstancia anterior, y el valor del límite inferior del IC para la RAR es inferior al ECI. En este caso no hay ningún problema, dado que el límite superior del IC de la RAR será compatible con un efecto terapéutico mucho mayor al encontrado por el EC.

Los EC con las características anteriores se propone clasificarlos como EC IA, para la aplicación de sus resultados a la práctica clínica.

Si se considera 2,5% como el efecto clínicamente importante en el MA17, los resultados de este estudio son estadística y clínicamente importantes, ya que la RAR encontrada fue de 6% y el límite superior del IC indica que el beneficio del letrozol es compatible con una RAR hasta de 7,6%.

Sin embargo, si la RAR y el límite superior del IC para la RAR es menor que el ECI, los resultados encontrados por el ensayo clínico son estadísticamente significativos pero no es un ECI (figura 2, EC IC).

Los EC con estas características se propone clasificarlos como EC tipo IC, para la aplicación de sus resultados en la práctica clínica.

Cuando la RAR está por debajo del ECI, pero el límite superior del IC es mayor al efecto clínicamente significativo, los resultados del ensayo clínico son estadísticamente significativos y compatibles con un ECI (figura 2, EC IB).

Los EC compatibles con ECI se propone clasificarlos como EC tipo IB, para la aplicación de sus resultados en la práctica clínica.

La razón para clasificar a los EC con resultados estadísticamente significativos como tipo I es para indicar que son estudios nivel I de evidencia y con poca probabilidad de ERROR TIPO I. El motivo para catalogarlos como A, B y C es para expresar el grado de aplicabilidad del EC en la práctica clínica.

Con experimentos clínicos tipo IB y en especial los de tipo IC, se plantea trasladar sus resultados a la práctica clínica con gran precaución, ponderando el pequeño efecto encontrado con el tipo de desenlace evaluado, costos y toxicidad de la terapia. Igualmente, sería válido trasladar sus resultados a grupos de mayor riesgo.

En este contexto es interesante analizar los resultados del estudio ATAC (Arimidex, Tamoxifeno solo o en combinación) que comparó tamoxifeno, anastrazol o la combinación de ambos agentes como terapia endocrina adyuvante en pacientes con cáncer temprano de seno (14, 15).

El desenlace primario del ATAC fue la supervivencia libre de enfermedad. Con sólo una mediana de seguimiento de 33,3 meses, los resultados del estudio ATAC fueron publicados en junio del 2002.

Se encontró que la supervivencia libre de enfermedad a tres años fue de 89,4% para anastrazol y 87,4% para tamoxifeno, con una RAR del 2% (hazard ratio 0,83 [IC 95% 0,71-0,96], p=0,013).

Los límites de confianza de 95% para la RAR van de 0,4 a 3,5% (RAR 2%; IC 95% 0,4 a 3,5%). Una vez establecido el ECI de 2,5% se puede indicar que el efecto terapéutico (RAR) encontrado en el ATAC estuvo por debajo del ECI y que el valor del límite superior del intervalo de confianza estuvo por encima del ECI.

Se podrían considerar los resultados del ATAC como estadísticamente significativos y compatibles con un ECI y clasificar este estudio como EC tipo IB.

La tabla 6 resume los principales aspectos para evaluar un EC para la toma de decisiones en la práctica clínica.

Un número importante de experimentos clínicos es diseñado para encontrar diferencias entre los tratamientos evaluados (EC comparativos).

El estudio se considera negativo si no es posible rechazar la hipótesis nula de diferencia entre los tratamientos, debido a un valor de p mayor o igual a 0,05. Sin embargo, estos estudios pueden tener poco poder para detectar diferencias clínicamente importantes en sus efectos terapéuticos.

Un tipo de error que se puede cometer consiste en concluir erróneamente que no existen diferencias entre los tratamientos evaluados cuando en realidad sí las hay (conclusión falsa negativa).

Es necesario distinguir entre un estudio falso negativo, en el cual la diferencia entre los tratamientos no alcanza significancia estadística debido a un tamaño de muestra inadecuado, y un estudio verdaderamente negativo que tiene suficiente número de sujetos en el estudio para detectar una diferencia clínicamente importante si ésta hubiera existido. Ahora, ¿cómo se puede diferenciar un EC falso negativo de uno verdaderamente negativo? En esta situación es preciso evaluar el límite superior del IC para la RAR del estudio.

Si el valor del límite superior del intervalo de la RAR es menor que el ECI, el EC puede considerarse verdaderamente negativo (figura 3).

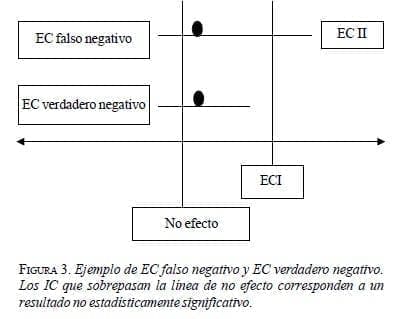
Si por el contrario, el límite superior del IC para la RAR se localiza por encima del ECI (figura 3, EC II) el estudio no puede considerarse negativo, sino más bien que carece de poder para detectar diferencias clínicamente importantes.

Se propone clasificar los EC negativos como EC tipo II para indicar que tienen alta probabilidad de ERROR TIPO II, para la aplicación de sus resultados en la práctica clínica. Como también que las conclusiones emanadas de este tipo de EC sean tomadas con gran precaución.

La tabla 7 contrasta las conclusiones derivadas de la interpretación de los EC con base en la significancia estadística y las conclusiones a partir de los IC.

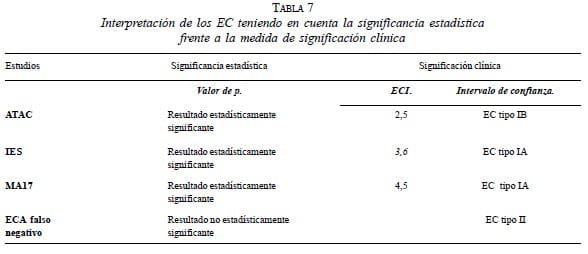
La significancia estadística con base en el valor de p divide los resultados de un EC en estadísticamente significantes y no estadísticamente significantes. Esta dicotomía de los resultados de un EC tiene dos limitaciones importantes:

1. Un resultado estadísticamente significativo no indica si el efecto terapéutico de una terapia es importante o no.

Un resultado estadísticamente significativo no implica importancia clínica por lo que éste podría no tener trascendencia en la práctica médica.

2. La interpretación de un EC únicamente con base en la significancia estadística de sus resultados podría conducir a conclusiones erróneas acerca de la nueva terapia: el error tipo II.

Siempre es necesario recordar que un valor muy pequeño de p no da indicio de la importancia clínica del efecto encontrado y un valor de p grande no indica equivalencia entre dos o más tratamientos (16).

Existen otras medidas de significación clínica como: gráfico del valor p frente a reducción absoluta del riesgo (17) y el análisis Bayesiano (18).

La descripción detallada de estas últimas medidas de significación clínica está fuera de los objetivos de esta revisión, por lo cual se remite al lector interesado en estas medidas a las referencias citadas.

Un criterio importante para considerar en la toma de decisión clínica es la preferencia del paciente por su tratamiento. La gran difusión y acceso a la información médica permite a los pacientes estar al tanto de las últimas innovaciones terapéuticas, lo cual los hace más autónomos en la toma de decisiones (19).

Los IC, como medida de significación clínica se deben considerar complementarios a otros criterios clínicos previamente establecidos: que los resultados de la terapia sean generalizables al paciente en particular, que la terapia produzca resultados clínicamente importantes para el paciente y que sean factibles de aplicar, y que se valoren los riesgos y costos de la nueva terapia (20).

El propósito de esta revisión estuvo dirigido a clarificar algunos de los aspectos estadísticos más importantes en la interpretación de los ensayos clínicos, y proponer unas herramientas de juicio clínico para la toma de decisión sobre la introducción de una nueva terapia a la práctica clínica: medida de significación clínica.

Esta revisión no pretende que los IC sean tomados como solución definitiva a la difícil tarea de la evaluación del beneficio de un tratamiento, sino la de estimular y suscitar más discusión sobre este tema.

Abstract

The evaluation of the beneficial effects of a particular therapy is mandatory before deciding on a new treatment modality. Clinicians that utilize the results of clinical trials to guide their practice need reliable tools for the evaluation of the clinical relevance of statistically significant results prior to the introduction of new cancer therapies. The purpose of this review is to propose the confidence intervals as useful tools to determine the clinical relevance of a treatment modality. The confidence interval attenuates the interpretation of clinical experiments solely on the basis of statistical criteria.

Key words: clinical significance, p value, confidence interval.

Referencias

1. LAUPACIS A, SACKETT DL, ROBERTS RS. An assessment of clinically useful measures of the consequences of treatment. N Engl J Med 1988; 318: 1728-1733.
2. MOHER D, DULBERG CS, WELLS GA. Statistical power, samplesize, and their reporting in randomized controlled trials. JAMA
1994; 272: 122-124.
3. CHAN KBY, MAN-SON-HING M, MOLNAR FJ, et al. How well is the clinical importance of study results reported? An Assessment of Randomized Controlled Trials. CMAJ 2001; 165: 1197-1202.
4. RESTREPO MM, GÓMEZ C. Sesgos en diseños analíticos. Rev Col Psiqui 2004; 33: 327-335.
5. GUYATT GH, SACKETT DL, COOK DJ. Users’ guides to the medical literature. ii. how to use an article about therapy or prevention. A. Are the results of the study valid? evidence- based medicine working group. JAMA 1993; 270: 2598-2601.
6. ROTHMAN KJ, GREENLAND S. “Approaches To Statistical Analysis”. En: Rothman KJ, Greenland S. Modern Epidemiology. Lippincott- Raven, 1998; 183-199.
7. STERNE JAC, SMITH GD, COX DR. Sifting The evidence{—}What’s Wrong with significance tests? another comment on the role of statistical methods. BMJ 2001; 322: 226-231.
8. BROWNER WS, NEWMAN TB. Are all significant p values created equal? the analogy between diagnostic tests and clinical research. JAMA 1987; 257: 2459-2463.
9. CASTAÑEDA JA, GIL JF. Una mirada a los intervalos de confianza en investigación. Rev Col Psiqui 2004; 33: 193-201.
10. JAESCHKE R, SINGER J, GUYATT GH. Measurement of health status. ascertaining the minimal clinically important difference. Control Clin Trials 1989; 10: 407-415.
11. BARRATT A, WYER PC, HATALA R, et al. Tips for learners of evidencebased medicine: 1. Relative risk reduction, absolute risk reduction and number needed to treat. CMAJ 2004; 171: 353-358.
12. COOMBES RC, HALL E, GIBSON LJ, et al. A randomized trial of exemestane after two to three years of tamoxifen therapy in postmenopausal women with primary breast cancer. N Engl J Med 2004; 350: 1081-1092.
13. GOSS PE, INGLE JN, MARTINO S, et al. A randomized trial of letrozole in postmenopausal women after five years of tamoxifen therapy for early-stage breast cancer. N Engl J Med 2003; 349: 1793-1802.
14. BAUM M, BUDZAR AU, CUZICK J, et al. Anastrozole alone or in combination with tamoxifen versus tamoxifen alone for adjuvant treatment of postmenopausal women with early breast cancer: first results of the ATAC randomized trial. Lancet 2002; 359: 2131-2139.
15. BAUM M, BUZDAR A, CUZICK J, et al. Anastrozole alone or in combination with tamoxifen versus tamoxifen alone for adjuvant treatment of postmenopausal women with early- stage breast cancer: results of the ATAC (Arimidex, Tamoxifen Alone or in Combination) trial efficacy and safety update analyses. Cancer 2003; 98: 1802-1810.
16. WHITLEY E, BALL J. Statistics review 3: hypothesis testing and p values. Crit Care 2002; 6: 222-225.
17. LEUNG WC. Balancing statistical and clinical significance in evaluating treatment effects. Postgrad Med J 2001; 77: 201-204.
18. BURTON PR, GURRIN LC, CAMPBELL MJ. Clinical significance not statistical significance: a simple bayesian alternative to p values. J Epidemiol Community Health 1998; 52: 318-323.
19. SERRANO M. La medicina basada en la evidencia: un nuevo paradigma en la interpretación de la información médica. Rev Colomb Cir 1999; 14: 134-139.
20. GUYATT GH, SACKETT DL, COOK DJ. Users’ guides to the medical literature. II. How to use an article about therapy or prevention. b. what were the results and will they help me in caring for my patients? Evidence-Based Medicine Working Group. Jama 1994; 271: 59-63.

Correspondencia:
EDUARDO TORREGROZA-DIAZGRANADOS, MD
torregrozad@yahoo.com.mx
Bogotá, D.C.